Pension Systems (Un)sustainability and Fiscal Constraints: A Comparative Analysis 2

Economics/Papers

Pension Systems (Un)sustainability and Fiscal Constraints: A Comparative Analysis 2

delphinee 2023. 8. 25. 02:31

Pension Systems (Un)sustainability and Fiscal Constraints: A Comparative Analysis 2

지난번에 모형과 측정 방법론, 여러가지 측도에 대해서 제시를 했다면 이번에는 양적 분석을 통해서, 질문들에 대한 답을 풀어나갈 수 있다. 시나리오와 counterfactual 를 기반으로 연금 개혁이 진행되었을 경우, 어떤 영향을 미치는지 보고자 한다.

[2기간 모형]

PS 와 PSEP의 **결정 요인 (determinants)**에서 연금 한도 (Pension Limit, PL) 를 계산하기 위해, 2기간 모형을 도입해서 통해 풀고 분석하여 그림으로 나타낼 수 있다.

두 기간으로 이루어진 모델에서는, 가계가 1기간에 일하고 2기간에 은퇴를 한다고 설정할 수 있다.
소비와 여가로부터의 평생 유틸리티는$U=\sqrt{c^{y}}+\beta \sqrt{c^{0}}+l$로 정의하고, 젊은 (young) 시기와 노인 (old) 시기의 **가계 예산 제약 조건 (budget constraints)**은 각각 $c^{y}+b=\left(1-\tau^{l}\right) w l$ 및 $c^{o}=(1+r) b+\theta w l$ 이다.
- 여기서 $b$는 정부 채권을 나타내고, 편의상 노년에 발생하는 연금 소득은 젊을 때의 노동 소득과 비례한다고 가정하며, 노동 생산성은 정규화되어 1로 둔다.
자본은 없으며 기술은 노동에 대해 선형 (linear)이기에, 즉, $y=A l$ 이다.
일반 정부 예산에는 채권과 노동 소득 과세 (income taxation)를 통한 소비 지출 (consumption expenditure)이 있다.
- 공적 연금 (Public pensions)은 노동 소득에 비례하며 **노동 소득에 부과되는 사회 보장 기여세 (social security contribution)**로 자금을 조달한다.
- 따라서 일반 정부 및 사회 보장 (social security) 예산 (budgets)에 대한 세수입은 각각 $t^{G}=\tau^{w} w l$ 및 $t^{P}=\tau^{p} w l$로 주어지고, 이 두 예산은 각각 $e=t^{G}$ 및 $\theta w l d=t^{P}$이다. 여기서 $e=g+[(1+r) d-1] b$이며, $d_{t}=N_{t-t} / N_{t}$는 의존률 (dependency ratio)을 나타낸다.
- 균형에서 노동 공급은 $l=\bar{l}\left(1-\tau^{w}-\tau^{p} \Phi\right)$ 이다. 여기서 $l=\bar{l}\left(1-\tau^{w}-\tau^{p} \Phi\right)$는 과세가 없을 때의 노동 공급을 나타내며 $\Phi=1-[d(1+r)]^{-1}$ 이다.

이제 문제를 풀기 위해서, 즉 사회 보험 예산을 극대화하기 위해 정부 제약 하에서 $\tau^{p}$ 비율을 선택하는 문제로 접근할 수 있는데, 이를 위해 Lagrangian은 다음과 같이 정의한다.

$$ \max _{\tau^{p}, \tau^{w}, \lambda} L=\tau^{p} w \bar{l}\left(1-\tau^{w}-\tau^{p} \Phi\right)+\lambda\left[\tau^{w} w \bar{l}\left(1-\tau^{w}-\tau^{p} \Phi\right)-e\right] $$

이 문제의 해 (solution) 조건은 다음과 같다.

$$ \tau^{p}=\frac{1-\tau^{w}-\lambda \tau^{w} \Phi}{2 \Phi}, \tau^{w}=\frac{\lambda-\tau^{p}(1+\lambda \Phi)}{2 \lambda} \\\lambda \geq 0 \\ e \leq t^{G}\\ \lambda\left(e-t^{G}\right)=0 $$

이 중 처음 두 조건은 Lagrangian을$\tau^{p}$ 및 $\tau^{w}$에 대해 미분한 결과이며, 마지막 세 조건은 전통적인 Kuhn-Tucker 조건이다.

일반 정부 예산이 bounding 제약이 아닐 때, $\lambda=0$ 이므로 소득 세율은 주어진 것으로 간주되며 사회 보험 예산을 극대화하는 세율은 $\widehat{\tau^{p}}=\left(1-\tau^{w}\right) /(2 \Phi)$ 이다.
반면에 $PL$은 현재 일반 정부 예산 규모를 유지하면서 사회 보험 예산 크기를 극대화하는 $\overline{\tau^{p}}$ 세율로 달성 된다. 소득 세율은 더 이상 불변이 아니다. $\tau^{p}$가 증가함에 따라 사회 보험 예산을 확장하기 위해 감소하며 $\lambda>0$이고 $e=t^{G}$인 경우 $\overline{\tau^{p}}<\widehat{\tau^{p}}$ 이다.
이는 제약된 최적화에서 $\tau^{p}$가 증가하면 사회 보험 예산을 확장하기 위해 ⇒ 노동 공급이 감소하며 정부는 일반 정부 예산 규모를 유지하기 위해 ⇒ 소득 세율을 조정해야 하기 때문이다. ⇒ 이로 인해 노동 공급이 더욱 감소하게 되어 연금 예산을 최대화하는 사회 보험 세율이 제한되지 않은 경우보다 줄어들게 된다. (라퍼 효과) 위에서 결정된 균형 solution을 사용하여 $PS$는 다음과 같이 계산할 수 있다.여기서 $l_{PL}$은 $\tau^{p}=\overline{\tau^{p}}$ 일 때의 노동 공급을 나타낸다.

$$ PS=100\left(1-\frac{\tau^{p} l}{\overline{\tau^{p}} l_{PL}}\right) $$

여기서 $l_{PL}$은 $\tau^{p}=\overline{\tau^{p}}$ 일 때의 노동 공급을 나타낸다.

(그림 해석) 위 그림은 PS와 PSEP의 결정 (determination)을 보여준다. 위쪽 왼쪽 패널은 $\tau^{p}$를 증가시키면서 일반 정부 예산의 규모를 유지할 때, 균형 노동 공급이 감소함을 보여준다 (왼쪽 축, 파란색). 동시에 소득 세율 $\tau^{w}$이 증가한다 (오른쪽 축, 빨간색). 녹색 점은 $\tau^{p}$ 보정을 위한 균형 solution 으로서 노동 공급이 0.25가 되도록 보정한 값을 나타낸다.이 균형 쌍은 $\left(\tau^{p }, l^{}\right)$로 표기된다. 빨간색 점은 경제가 $PL$ (연금한도)에 도달했을 때의 사회 보험 세율 및 최소 노동 공급을 나타내며, 균형은 $\left(\overline{\tau^{p}}, l_{PL}\right)$로 표기되며, $\overline{\tau^{w}}$는 $PL$ 균형에서의 소득 세율을 의미한다.

위쪽 오른쪽 패널은 $\tau^{p}$가 0에서 $\overline{\tau^{p}}$ 까지 증가함에 따라 사회 보험 예산이 어떻게 확장되는지를 보여준다. 균형 $\tau^{p *}$ 및 $PL$에서 암시되는 **누적 연금 지출 (A P E)**은 수직 축에 표시된다. 이는 각각 $\left(\tau^{p }, l^{}\right)$ 및 $\left(\overline{\tau^{p}}, l_{PL}\right)$에서의 사회 보험 예산 규모를 나타낸다.

아래쪽 왼쪽 패널은 PS (Pension Space) 의 균형 세율 $\tau^{p *}$ 변화에 대한 변화를 보여준다. 인구 구조, 선호도, 기술 및 일반 정부 예산을 나타내는 매개 변수가 주어지면 **Pension Limit (PL)**은 고유하게 결정된다. 따라서 균형 $\tau^{p *}$이 증가함에 따라 PS가 축소됩니다.

아래쪽 오른쪽 패널은 평균이 0.2이고 표준 편차가 0.2인 독립적인 분포에서 추출한 1000개의 인구 성장률의 누적 밀도 함수를 보여준다. 수직 빨간색 선은 PS=0인 지점을 표시한다. 이 지점을 수직 축에 투영하면 PSEP가 얻어지며, 이는 경제 환경 및 재정 및 연금 정책 조치에서 PS가 고갈되는 인구 구조 불확실성 (demographic uncertainty)으로 인한 위험을 나타낸다.

[캘리브레이션 및 데이터]

캘리브레이션 (calibration)은 각 나라에 대한 **균형 상태 (steady state)**를 근사화하기 위해 설계되었으며 1980년부터 2020년까지의 데이터 평균을 기반으로 한다.
외부 데이터를 사용하여 각 나라에 대해 보정된 매개변수 값을 나타낸다. 모델 내에서 기간 t는 1년을 의미한다. 신생아 (Newborns)의 실제 연령은 20세로 가정되어 s = 1에 해당하며, 94세까지 실제 연령을 가지며 T=75이라고 놓는다.
- **은퇴 연령 $T^W$은 OECD (2021)에서 얻은 2014년, 2018년 및 2020년의 남성의 실제 은퇴 연령의 평균으로 계산. 인구 증가율 n은 UN (2022)에서 얻은 1980년부터 2020년까지의 연간 인구 증가율의 평균으로 계산
- 생존 확률 $\phi_{st}$는 UN (2022)에서 얻은 남녀 합한 평균 수명 데이터 (20세부터 95세까지)를 기반으로 계산되며, 각 나라별로 1980년부터 2020년까지의 평균 생존 확률을 사용

매개 변수 $\alpha$와 $\delta$는 국가에 따라 다르며, Trabandt와 Uhlig (2011)에서 가져온 값들이다. 생산성 성장률 $g_{A}$은 각 나라의 1980년부터 2020년까지의 실질 GDP per capita 평균 성장률과 일치하도록 설정한다. 이는 OECD (2022)에서 얻은 데이터를 사용하여 시장 가격에서의 연간 명목 국내 총생산 값을 해당 디플레이터 (deflator)로 스케일링한 다음 총 인구로 나누어 계산
노동소득에 대한 세율 $\tau^{l}$, 자본에 대한 세율 $\tau^{k}$, 소비에 대한 세율 $\tau^{c}$은 Mendoza et al. (1994)의 방법을 개정한 Carey와 Rabesona (2003)의 방법을 사용하여 계산

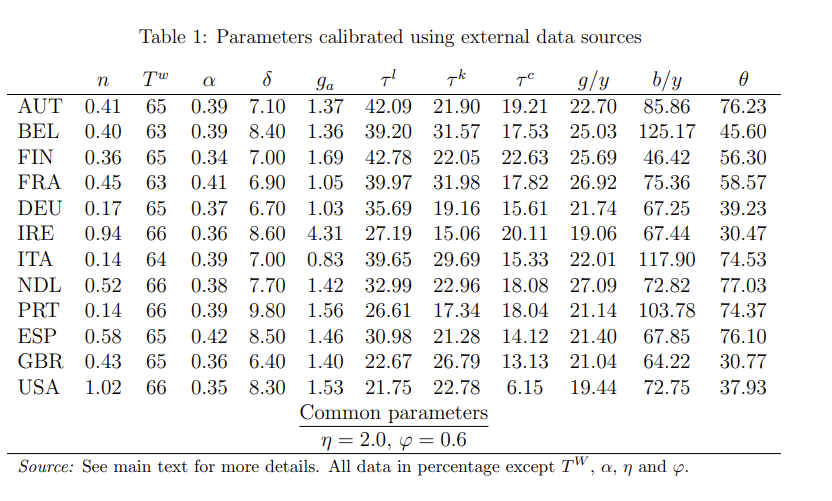
(표 해석) 정부 지출 대 GDP 비율 $g/y$은 시장 가격에서의 총 국가 최종 소비지출 (nominal general government final consumption expenditure) 및 고정 자본 형성 (fixed capital formation) 의 연간 합계를 총 국내 총생산 값에 대한 비율로 계산된다.

GDP 대 부채 비율 $b/y$는 1980년부터 2020년까지의 일반 정부 총 금융 부채의 평균(government gross financial liabilities) 을 GDP의 백분율로 측정
연금 대체율 (Pension replacement rates) $\theta$은 OECD (2021)에서 얻은 평균 남성의 평균 소득을 기반으로 2014년, 2018년 및 2020년의 평균 연금 대체율

2020년부터 2050년까지의 PS를 계산하고, 이 기간동안 PSEP의 변화를 추정하기 위해서, 인구 성장과 생존 확률에 대한 예측을 활용한다.

evolution of the population growth rates (n) ** 빨간 선은 세계 인구 증가율이며, 40년 rolling 평균

.(그림 해석) 각 나라의 인구 증가율을 보여준다. 2021년 이후 데이터는 중앙값 projection이다. 세 가지 패턴을 찾을 수 있는데 1) 선택된 대부분의 나라는 세계에서 가장 노령 인구를 많이 가진 나라 중 하나로, 앞으로 30년 동안 매우 빠르게 노령화될 것으로 예측된다. 2) 노령화 속도는 나라마다 매우 이질적이다. 예를 들면, 독일, 이탈리아, 포르투갈 및 스페인은 2050년까지 음의 인구 성장률을 가질 것으로 예상되고, 다른 모든 나라는 동일한 기간 동안 약 20%에서 87% 정도의 인구 성장 감소를 경험할 것으로 예상된다. 3) 앞으로 30년 동안 인구 역학에 대한 불확실성이 크다는 것이다.

국가들 간에 거시 경제적 특성, 공공 연금 제도, 인구 구조, 노령화 예측 및 불확실성에서 상당한 차이를 보인다. 이런 국가의 다양성 다양성은 공공 연금 정책 개혁의 거시 경제 및 복지 효과가 그것이 실행되는 특정한 경제 조건에 의존하기 때문에 큰 의미를 가지게 된다.

Differences in PS Magnitude among Nations

(그림 해석) 예를 들어, 미국의 경우, 연금 지출이 GDP의 5.32%를 차지하고, PL에서는 12.31%이다. PS는 PL에서 사용되지 않은 비율로 56.77%이다. 서로 다른 국가 간에 PS가 큰 차이가 있고, 2020년에 대한 값에는 5%~57$%까지 다양하게 나타난다. 미국, 영국 및 아일랜드는 40% 이상이며, 프랑스 및 이탈리아, 벨기에는 10% 미만이다.

PS와 PL의 차이를 설명하는 두 가지 주요 요인은 노동 소득 과세와 연금 제도의 관대함 (generosity of the pension system)을 보여준다.

PS가 낮은 네 나라는 **가장 널널한 대체율 (replacement rates)**과 가장 높은 **사회 보장 세율 (social security tax rates)**을 가진다.
일반적으로 PS는 노동 소득 세율(labour income) ($\tau^l$)이 낮은 국가에서 크고, less generous한 연금 체계 ($\mathrm{Pen} / Y$) 가 커진다. 그 이유는 국가들은 더 높은 연금 지급을 지원할 만큼의 여유가 있기 때문이라 재정 (finance)의 필요성이 덜 하기 때문이다.
$\tau_{t}^{w}=\tau_{t}^{l}-\tau_{t}^{p}$ (income tax rate) 는 $\tau_t^p$ 가 PL에 접근함에 따라 증가하는데 연금 지급 (pension payments)이 증가하면, 저축과 자본이 따라서 감소한다. 이로 인해 노동 공급이 감소하고, 총 소비, 소득 및 세수입이 감소한다.
따라서 사회 보장 예산의 크기가 PL에서 최대화 되기 위한 문제에서, 정부 예산 제약의 크기가 불변하는 조건을 만족 시키기 위해, 세율 (tax rate) $\tau^w$ 를 증가시켜야 한다.

중요한 것은 캘리브레이션 값을 다른 값으로 대체할 때 어떻게 변화하는지 살피는 것이다.

(1) (노동)

먼저 노동 탄력성 (Frisch labour elasticity) $\varphi$ 와 생산 profile (age-productivity profile) $\bar{y}^{s}$ 을 보았을 때, (1) “높은” 노동 탄력성 (0.6 → 1)과 (2) “hump-shaped” 세대 생산성은 PS 를 낮추는 요인으로 작용 (각각 평균 4.7% ; 1.8% 감소) 했다. 모형이 다시 calibration 되는 것이기에 $\operatorname{Pen}{t}, \tau{t}^{l} \text ,\tau_{t}^{p}$ 는 영향이 없다. 또한 노동 탄력성이 증가하기에 PL이 감소하고, 세율이 증가한다는 점을 확인할 수 있다.

** 왜 hump-shaped 생산성이 PS 를 낮추냐면, 일을 많이 하는 20-39세의 사람들이 다른 연령대에 비해서 tax를 덜 지불하기 때문이다.
다만, 이 두 효과가 상쇄되어 PS 에 미치는 효과는 불분명하다.

(2) (경제 성장과 정부의 부채)

생산 증가율 $g_{A}$ 를 1%p 올리고, $b / y$ 를 20%p 올렸을 때, 국가간 순위는 변하지 않는다. 성장률이 높을수록 PS가 증가하고, 높은 부채가 있을 수록 PS가 줄어든다.

⇒ 즉 위의 결과 값이 robust 함을 보여준다.

[Counterfactual]

위의 인구 성장률을 바탕으로, 네 가지 다른 정책 시나리오 하에서 PS가 어떻게 변화하는 지를 계량화 할 수 있다. 첫 시나리오는 정책 변경을 하지 않을 경우, 나머지 세 가지 시나리오는 공공 연금의 지속 가능성 (sustainability of public pensions) 을 개선하는 개혁 (reforms) 요소를 포착하는 대상으로 반사실적 (counterfactual)인 정책 개입을 했을 때 PS 와 PSEP의 반응을 분석한다. $\tau^{c}, \theta, T^{W}$ 세 가지 정책 변수의 변화 정도를 파악할 수 있다.

1) 정책 변경이 없는 시나리오
2) P1 (정책1) 간접세 (indirect taxes) 5% 증가
3) P2 (정책2) 연금 대체율 (replacement rate of pension) $\theta$를 10% 감소시키는 정책
4) P3 (정책3) 은퇴 연령 (age of retirement) $T^{W}$를 2년 연장하는 정책

1) 정책 변경이 없는 시나리오

(i) 인구 성장률과 생존 확률이 매년 유엔 (2022)의 중앙 예측에 따라 변경되며, (ii) 각 나라가 노후 가계에 대한 연금 지불인 $pen_t$와 은퇴 연령 $T_W$를 2020년 수준으로 유지하면서, 연금의 높은 비용을 세금 $τ_p$ 인상으로 지원한다고 가정
각 나라에서 PSEP의 해당하는 변화는 다음과 같이 계산
- 먼저, 기준 보정을 사용하여 2020년부터 2050년까지 PS를 계산하지만, 각 해의 인구 성장률과 생존 확률은 유엔 (2022)의 예측의 5번째, 20번째, 80번째 및 95번째 백분위 수에서 가져온다. ⇒ 이것들은 중앙 인구 예측을 기반으로 한 PS의 시계열과 결합되어 각 해별 PS의 커널 (kernal) 누적 밀도 함수를 추정하는 데 사용
- 이 분포에서 PS가 0이 되는 확률을 PSEP로 추정합니다.

(왼쪽 그림; PS) 시간이 지남에 따라 인구 노령화로 인해 공공 연금의 비용이 증가할 것이라는 것은 예상할 수 있다. 따라서 PS 는 당연히 줄어들 것이다. Figure 3은 정책 개혁이 없는 시나리오에서 2020-2050년 동안 각 국가별로 PS (검은 선)가 어떻게 변화하는지 보여준다. 또한 그래프에는 연금 지출과 PL 두 가지 주요한 P S 결정 요인도 포함되어 있습니다.

시간이 지남에 따른 PS의 감소는 PL (빨간 점선; 평평한 모습을 보임) 보다는, 대부분 연금 지출의 변화 (aggregate pension expenditure) 에 의해 주로 결정된다. 노령화가 진행될수록, 이 연금 지출이 증가할 것이다.

그 이유로는 1) 연금 한도 (PL)에서는 최대 수준의 사회 보장 세율이 $\bar{\tau}_{p}$ 거의 상수이고 2) 노동 공급 L이 시간에 따라 감소하고, 임금인 w는 증가하기 때문이다.

(오른쪽 그림; PSEP) 각 국가별로 2020-2050년 동안 추정된 PSEP를 나타내고, 감소 속도를 확인할 수 있다. 대부분의 국가에서 이후 30년 동안 추가 노동 소득 과세로 공공 연금을 지원할 여지가 거의 없다는 것을 보여준다.

이제는, 연금 개혁이 PS의 크기, 시간 경과에 따른 변화 및 미래 어느 시점에서 고갈될 가능성에 어떤 영향을 미칠지 살펴보고자 한다. 연금 정책 개혁은, 동일한 유형의 개혁이 각 국가의 PS와 PSEP에 다른 영향을 미치기에 모든 나라에 공통적인 해결책이 될 수 없다.

2) P1 (정책1) 은 간접세 (indirect taxes)을 일부 자금화하여 연금 지출의 효과를 고려

즉, $\tau^{c}$를 5% 증가시키는 것을 연구

3) P2 (정책2) 연금 대체율 (replacement rate of pension) $\theta$를 10% 감소시키는 정책

4) P3 (정책3) 은퇴 연령 (age of retirement) $T^{W}$를 2년 연장하는 정책

(왼쪽 그림; PS) 2020년부터 2050년까지 세 가지 형식화된 정책 개혁 P1, P2 및 P3에 따른 PS의 변화를 나타낸다. 오스트리아, 프랑스, 이탈리아, 네덜란드 (파란 점선) 는 노후 연령을 2년 연장하는 정책 P3에서 최대 PS에 달성한다. 포르투갈 스페인은 연금 대체율을 10% 감소시키는 P2정책 (빨간 점선)에 의해서 가장 큰 PS 달성이 가능하다는 것을 알 수 있다. 나머지 6개 국가에서는 소비 과세를 5% 인상하는 정책인 P1 (빨간 실선)에서 가장 큰 PS가 달성됨을 확인할 수 있다.

이는 왜곡된 소득 과세를 감소시키고, 노동 공급을 촉진하여 연금 지출을 줄이기 때문에 PS를 정책 변화가 없을 시보다 증가하게 된다.
(메커니즘) P1과 P2는 각 기간에 노동 공급을 강화시키며, P3는 주로 광범위한 규모에서 노동 공급에 영향을 미친다. 따라서 이 모든 경우는 총 생산을 증가시킨다. 따라서 GDP 대비 연금 지출 비율이 감소하고 이로 인해 PS가 증가하는 것이다.
또한, 정책 P2에서는 PS 상승 변화가 특정 시점에서 가속화 되는 경우가 있는데, 이는 예상한 인구 성장 중앙값이 크게 감소하는 연도에 발생하게 된다. 이에 연금 대체율을 감소시키는 정책은 노화에 대해서 연금 제도를 더 견고하게 만드는 것처럼 보이기도 한다.

(오른쪽 그림; PSEP) 정책 개혁에 따른 PSEP의 변화를 제시한다. 연금 개혁의 효과로 PSE는 각 국가에서 감소하게 된다. 확실히 개혁이 PSEP에 미치는 영향은 PS에 미치는 영향보다 작다는 것이 관찰된다. 이는 주로 PS 변화가 중앙 인구 증가율 예측에만 의존하기 때문이다.

다만, PSEP 추정치는 예상 인가 증가율의 전체적인 경향성에 의존한다. 따라서 PSEP는 PS와 비교해서 더 신뢰할만한 지표가 될 수 있다. 인구 통계의 불확실성을 감안하더라도, 인구 전체의 경향을 반영하는 게 더 정확하기 때문이다.