Does Arbitrage flatten demand curves for stocks? 2

 

 

수요 탄력성과 차익 거래 위험 (arbitrage risk) 를 어떻게 엮어서 설명할까!?

 

기본적으로 새롭게 구성한 측정치를 보여주고, 이 측정치로 무엇을 어떻게 설명할 것인지에 대한 틀은 크게 바뀌지 않는다.

 

Does Arbitrage flatten demand curves for stocks? (2014)
저자 : Jeffrey Wurgler, Zhuravskaya
저널 : JFE

 

이 논문에서는, 초과 수요 충격 (excess demand shock)에 따른 가격이, 실제로 (1) 충격의 크기 (size of shock)와 주식의 (2) 차익거래 위험 (abitrage risk)에 따라서 증가하게 된다는 것을 데이터로 보여준다.

 

 

(검증) “S&P 500 지수에 추가가 된 주식” 가격의 반응을 cross-section으로 확인해 봄.

• 만약 index에 추가되면, index를 추종하는 펀드에 의해서 해당 주식이 대량으로 매수가 된다. 일반적으로 인수 합병이나 파산으로 인해서 다른 주식이 제외될 때만 지수에 새로 추가되기 때문에, 추가적인 주식에 대해서 index fund 수요가 갑자기 증가하는 것은 사실은 본질적으로는 “외생적인 수요 충격”이라고 할 수 있다. (유용한 정보가 없다는 말임)

 

(데이터 및 전처리) 1976년과 1989년 9월 데이터

• ** 최근에는 index 변경이 사전에 발표되어 차익거래자 (arbitrageur)들이 발표일 (announcement date)과 유효일 사이 (effective date)의 기간 사이에 index fund를 선점 (front-running)할 가능성이 높기 때문에 혼란 (confounding) 효과가 있을 수 있어 정확하지 않아 이 부분 제거

 

(기존 논의)

• s&p500 에 추가된 주식의 가격이 해당 변경일에 평균 3% 상승한다고 보았고, shleifer는 이 결과가 하향 경사의 수요 곡선의 내용을 반영한다고 주장
• 아마도 S&P 500에 추가가 된 사실이 실제로 회사의 전망에 대한 긍정적인 소식을 반영하는 것일 수 있다. 그러나 이것은 추가 효과가 시간이 지남에 따라 강력하게 증가한 이유를 설명하지는 못한다.
• 추가에 따른 효과를 다르게 설명하는 방식 중 또 다른 하나는, index 펀드에 연관된 유동성으로 인해 미래 거래 비용 감소가 반영된 것일 수 있다는 점이다.
  • 그러나 Beneish와 Whaley (1996)는 S&P 500 추가 후에 매수-매도 스프레드가 영구적으로 감소하지 않았다고 발견

 

 

---

 

 

[결과1. 측정치(measure)에 대한 정보]

 

이번 모형은 S&P 500에 추가된 각 주식에 대해, index fund 수요 충격의 “(1) 크기(sizse)”와 주식의 “(2) **Arbitrage risk”**를 측정 (measure)한다.

• (2) Arbitrage risk의 경우는, “추가된 주식”에 대해 $1의 매수 (short) + “대체 포트폴리오’에 대해 $1의 매도 (long)를 하는 순투자 포트폴리오(zero-net-investment portfolio)의 “과거 분산 (historical variance)”으로 측정

 

 

(측정; measure) 리스크 수준은 다르지만, 그 외의 것들에서 유사한 특성을 가지는 두 주식을 선택하고, 정보가 없는 초과 수요 충격을 동일하게 가하고 그들의 가격 반응을 비교하는 방식을 택한다.

 

1. 차익 거래 리스크 차익거래 리스크가 높은 주식이라면, 수요 곡선이 정말로 더 가팔라져서 더 큰 가격 반응이 있어야 함

• 주식의 공급 곡선은 해당 시점에서 고정되어 있으므로, 주식의 총수요 곡선의 기울기와 이동의 크기에 의해 결정이 되기 때문
  • 차익거래 리스크를 측정하기 위해 모형은 해당 주식에 대한 $1의 매수 포지션과 closer substitutes에 대한 $1의 공매도 포지션을 가진 포트폴리오의 분산을 사용
  • S&P 500 추가 설정에서는 추가된 주식을 공매도하고 대체재에 투자하는 것이 자연스러우므로, 변동은 $\operatorname{Var}\left(R_{i}-R_{j}\right)=\operatorname{Var}\left(R_{j}-R_{j}\right)$ 이라고 설정

 

2. 충격 사이즈: Standard and Poor's가 제공한 S&P 500에 indexed된 모든 펀드의 누적 크기 (cumultavie size)에 의존

• 수요 충격 크기를 주식의 자본화 (firm’s capitalization)를 기준으로 한 백분율 (percent shock)으로 추정

 

 

(방법론; Regression) 이벤트 당일날의 수익 결정 요소에 대한 회귀 분석 (regression)을 보여주고, 차익거래 리스크와 충격 크기의 영향이 수익률에 미치는 영향은 20 거래일 이상 지속되지만 그 이후로는 의미 있는 추론을 하기 어렵다는 것을 보여준다.

• (기초통계) 259개 주식에 대한 이벤트 당일의 수익 평균은 3.29%이고 (표준편차 = 2.32%), 시장 평균 수익률은 3.16% (표준편차 = 2.29%)
• 차익거래 리스크인 A와 수요 충격 크기인 S이라 할 때, 대체재 (substitutes)로는 (1) 시장 포트폴리오와 (2) 세 가지 주식 (산업 및 size, Book to market 이 유사한)을 활용하고, 이로 인해 meausre 하는 차익거래 리스크는 각각 A1과 A2이라고 함
  • 이때, A2의 경우, Church's Fried Chicken를 살펴볼 수 있다. Church's는 1977년 11월 16일에 S&P 500 지수에 추가되었으며 1989년 3월 1일에 인수가 되면서 제거된 케이스
    • Church의 산업에서 CRSP 주식을 정렬해 두고, (1) 시장 market capitalization과 Church의 market capitalization의 절대값 차이와, (2) 시장의 book-to-market 비율과 “Church”의 book-to-market 의 차이에 따라서 다섯 개의 분위로 나눈다.
    • 다음을 이용해서 정렬을 하고, 상위에 있는 3개의 주식을 고른다.
    • 두 개 quantile에서 같은 가치를 가지고 있는 주식의 연결고리 (ties)를 깨기 위해서, 자본 차이가 가장 작은 것을 선정 

• 마지막 단계로, 제로-순자본 투자 포트폴리오의 분산을 결정
  • 이때의 포트폴리오는 Church's에 대해 $1을 long + 세 가지 대체 상품 (순 합이 1달러 숏 포지션) 주식에 대한 $1의 short 포지션을 가짐 (단, 단기 포지션은 전체적인 포지션의 분산을 최소화하도록 설정)
  • 이 세 기울기 계수의 합을 일치시키는 제약을 두지 않고도 zero net 투자를 유지

• 다음 모형은 이벤트 전 calendar day window [-365,-20]의 일일 데이터를 사용하여 추정
  • $R_{\text{Church's,t}}$는 Church's 주식의 t일자 excess 수익률
  • $R_{\text{ft}}$는 무위험 이자율(보통 단기 국채 수익률)
  • $R_{\text{Wendy's,}}, R_{\text{Morrison, t}}, R_{\text{Friendly's,}}$는 각각 Wendy's, Morrison, Friendly's 주식의 t일자 excess 수익률
  • 0.108, 0.259, 0.109는 각각 Church's 주식 excess 수익률을 세 대체 주식 excess 수익률의 조합으로 나타내는 회귀 계수

$$ \left(R_{\text {Church's, }}-R_{\mathrm{ft}}\right)= .108\left(R_{\text {Wendy's, }}-R_{\mathrm{ft}}\right) +.259\left(R_{\text {Morrison, } \mathrm{t}}-R_{\mathrm{ft}}\right)+.109\left(R_{\text {Friendly's, }}-R_{\mathrm{ft}}\right) $$

 

 

• 이를 차익거래 전략으로 보자면, Church's $1 long + T-bills $1을 short에 대해서
  • Wendy's $0.108을 공매도 +T-bills $0.108을 매수
  • Morrison $0.259를 공매도 + T-bills $0.259를 매수
  • Friendly's $0.109를 공매도 +T-bills $0.109를 매수

 

 

(arbitrageur risk measure) 두 종류의 주식별 차익거래기회 위험 (arbitrageur risk) 측정치 A를 도출

• $A_{1i}$는 $R_{it} - R_{ft} = \beta_{11}(R_{mt} - R_{f})$의 잔차 분산으로 정의
  • $R_{mt}$는 CRSP의 가중치 조정된 AMEX/NASDAQ/NYSE 지수의 수익률이고, $R_{f}$는 T-bill 수익률
  • ** $R_{f}$의 일별 값은 해당 월간 수익률의 적절하게 근사화
• $A_{2i}$는 모델 $R_{in} - R_{f} = \beta_{1i}(R_{wb1i} - R_{f}) + \beta_{21}(R_{wb2i} - R_{f}) + \beta_{3i}(R_{sub3i} - R_{f})$의 잔차 분산으로 정의
  • $R_{wb1i}$, $R_{wb2i}$, $R_{sub3i}$는 각각 산업, 크기 및 자산 대응되는 "대체" 주식의 수익률
    • 산업을 매칭하기 위해 Fama와 French (1997) 산업 분류를 사용
• $E_{1i}$는 "설명된" 분산으로 정의되며 $Var(R_{it} - R_{f}) - A_{1i}$입니다. $E_{2i}$도 유사한 방식으로 정의

요약 통계 : (1) 새로 추가된 주식의 “초과 수익률”의 총 분산 (2) 대체 주식의 수익률이 “설명”하는 총 분산의 절대량 및 비율

보다시피, 개별 주식이 완전한 대체품을 갖고 있지 않다는 점을 확인할 수 있다.

• 위험에 대한 측정치인 A1 및 A2는 크기가 유사하며 매우 상관 관계 (0.98)가 높고, 전체적으로 헷징하지 않는 것 (4행 $\operatorname{Var}\left(R_{\mathrm{it}}\right)$)에 비해 약간 높은 수준의 크기를 가짐 (Var 비교)
• (표의 마지막 네 행) 좋은 대체 상품이 일반적으로 투기적 수익률 (speculative return)의 분산을 5분의 1로 줄이고, 몇몇 주식은 최대 3분의 5까지 줄일 수 있다는 것을 보여준다.
  • 그러나 일부 주식에 대해 헷징은 본질적으로 불가능하고, 대체할 만한 증권이 없다.
  • 일반적으로, 소형 주식은 대형 주식보다 차익거래 리스크가 더 높고, 샘플에서 log(시장 가치)와 A 간의 상관 관계 (correlation)는 음(-)이고 매우 높은 유의성을 가짐

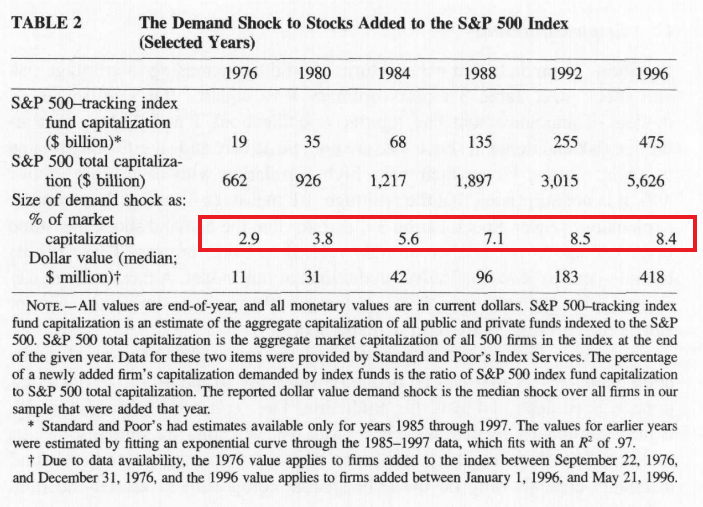
S&P 500은 가치 가중 지수이므로 S&P 500 지수로 인덱싱된 총 자산 대비 S&P 500 시가총액의 비율은 인덱스 펀드가 요구하는 각 포함 기업의 비율을 식별

• S&P 500 총 시가총액은 해당 연도의 말일에 인덱스의 모든 500개 기업의 시가총액의 종합
• ** 백분율은 추가된 S&P 500 지수 펀드 시가총액을 S&P 500 총 시가총액으로 나눈 것
• *** 수요 충격은 그해에 추가된 우리 샘플의 모든 기업에서 중간 충격

표를 보면, (1행) 1976년부터 1996년까지 인덱스 펀드는 19억 달러에서 475억 달러로 2,400% 성장했다. (2행) 동일한 기간 동안 S&P 500의 총 자본 시가총액은 6620억 달러에서 5626억 달러로 750% 성장했고, (3행) 추가된 기업의 자본 시가총액 중 인덱스 펀드에 의한 demand shock 크기는 1976년 약 3%에서 1996년에는 8% 이상으로 강력하게 성장

 

 

 

 

[결과2. 차익거래 위험 및 수요 충격 크기와 abnormal 수익률 간의 관계]

Test 를 하고자 하는 것과 OLS 를 어떻게 돌리는지, 변수의 proxy 데이터를 무엇으로 사용하는지 잘 확인해 보아야 한다.

• (4) 열은 이벤트 날의 수익률이 헷지 (hedge)할 수 있는 “risk component” (E) 에는 반응하지 않아야 하고, arbitrage risk 요인에만 반응을 해야 한다는 점을 잡아낸다. 여기서는 risk 요인을 이벤트 수익률과 관련이 없다고 보았다.
  • 평균 closed-end 펀드 discount는 closed end fund 위험 요인에서 헤징할 수 없는 곳에 의존
• (5) 열은 ommited variable h 에 의해서 상관관계가 있을 수 있기 때문에 arbitrage 위험 계수 (coefficient)가 biased 될 가능성이 있다는 점을 잡아낸다.
  • 다시 말해서, 극도로 비효율적인 시장 모형을 상상해보면, 총수요 곡선은 비-차익거래자의 믿음의 이질성에 의해서 전적으로 결정이 된다.
  • (방법론) 애널리스트의 예측치 I/B/E/S로부터 확인할 수 있는 “투자자 신념의 이질성 (heterogeneity)”을 proxy로 사용함 (analyst dispersion)
    • h에 대한 proxy가 이벤트의 수익률과 강력하게 관련되어 있지 않으며, 이를 제어하더라도 차익 거래 위험 (arbitrage risk)에 대한 계수를 감소시키지 않음을 볼 수 있다.
    • 다만, 이론적으로 모호한 관계가 있기 때문에 투자자의 믿음 effect는 약한 것으로 보이지만, 이질성을 측정할 수 있는 상황에서는 이질성이 수요곡선의 기울기에 영향을 미칠 수 있다는 것을 보여준다.
• (6) (7) 열은 ‘차익거래 위험’과 ‘충격의 크기’ 사이의 상호작용이 미치는 영향을 설명한다. 즉 비선형적인 부분을 설명한다.
  • 비차익거래자의 수요가 상태적으로 비탄력적 (inelastic) (h가 큼)일 때, 비-차익거래자는 index-fund에 주식을 공급을 하지 않는다. 오직 차익 거래자만이 수요 충격을 흡수한다.
    • 여기서 차익거래 리스크와 충격 크기의 상호작용이 매우 강력한 설명 변수로 작용하는데, 이는 위의 가설을 아주 잘 확인시켜 준다고 할 수 있다. (크기는 크고, 차익거래 리스크도 클 때)
• 또한 상수항 2%를 포함하고 있음에도 유의해야 한다.

⇒ 이는 즉, 차익거래가 주식의 수요 곡선을 평평하게 만들지 못하며, 이는 완전한 대체재가 없기 때문이라고 할 수 있다.

 

 

 

[결과3. abnormal 한 수익률 plotting]

또한 결과의 경제적 중요성 (economic signifiance)에 대해서 설명하기 위해 추가적인 연구를 한다.

이벤트 당일날의 효과 빠르게 다시 원래 상태로 돌아오는 지의 (reverting)여부를 확인하기 위해 누적된 주식의 평균 비정상 수익 (abnormal)을 plotting 해본다. (충격 크기 별로)

• 이를 통해, 결과가 일시적인 가격 압력 (price pressures)인지 아니면 실제로 장기간의 내려가는 수요 곡선인지를 확인할 수 있다.
• 다만, long-run inference에 대한 것의 설명은 아직 하기 어렵다. 평균 3%의 비정상적이 수익은 뉴스 등의 노이즈에 의해서 swanped 된다.

(왼쪽 그림; Shock size) 큰 충격이 큰 가격 반응을 유발하고, 평균은 20 거래일 이내에는 역방향으로 나타나지 않음을 확인할 수 있고, 누적 수익의 분산이 빠르게 증가하여 10일 이내에는 통계적으로 구별하기 어렵다. (오른쪽 그림; Arbitrageur risk) 고-차익거래 위험 주식이 더 큰 평균 가격 반응을 보인다는 것도 확인 가능하다.

또한 중요한 점은 부분 회귀가 완전한 회귀와 모형과 일관성이 있다는 것이다. 어떤 식으로든 차익거래자들은 평균적으로 이익을 얻게 된다.

 

 

 

[결과4. 수요 곡선의 기울기]

여기서는 회귀 결과에 내재된 총 수요 곡선의 기울기를 살펴보고자 한다.

• (탄력성) 수요의 가격 탄력성은 가격이 1% 증가할 때 수요의 퍼센트 변화인 수요에 대한 백분율 변화에 중점을 두는 것
  • complet market에서는 탄력성이 음의 무한대이다. 즉, 주식이 과대평가(과소평가)되어 있다면 투자자들은 무한한 양을 공매도하고(매수)하려고 할 것
• 이 모형에서 탄력성 측정치는 (% $\Delta x$ / % $\Delta P$), x의 주식 공급 곡선이 수직이기 때문에 과잉 수요(excess demand)로 볼 수 있다.
  • 즉, 가격 탄력성이 전체 주식의 변화로부터 식별될 수 있다는 것을 의미하며 수요 충격과 마찬가지로 적용
• (모형의 가정) 수요 곡선이 일정한 inelasticity를 가지며, 즉 가격이 1% 증가할 때 수요의 달러 변화가 일정하다는 것을 의미

(방법론) 이 논문에서는 위의 (8)열 즉, 차익거래 위험(arbitrage risk)의 25th 백분위수, 중앙값 및 75th 백분위수에 대한 주식의 내제된 탄력성 (implied elasticity)을 계산한다.

• median 값은 8.24 =1/(3.901 * .000311 * 100 *-1)이며,
  • 3.901은 (8) 에서 arbitrage risk와 percent shock의 상호 작용에 대한 계수
  • 0.000311은 표 2의 arbitrage risk 의 중앙값, 100은 백분율 변화를 퍼센트 변화로 전환하기 위한 decimal return (Scale factor) 이다.
  • -1은 percentage demand shock의 수용으로 인한 arbitrage와 non-arbitrage 수요의 percent 감소를 나타낸다.
• 25th 백분위수에 해당하는 주식은 탄력성이 -11.72로 훨씬 더 평평한 수요 곡선을 가지며, 75th 백분위수의 주식은 탄력성이 -5.57로 훨씬 가파른 수요 곡선을 가진다.

⇒ 즉 감소하는 수요 곡선을 보여줌