The Term Structure of Growth-at-Risk

The Term Structure of Growth-at-Risk (AER)
저자 : Tobias Adrian, Federico Grinberg, Nellie Liang, and Sheheryar Malik (2023)
분야 : Macro

 

 

 

[주요 내용]

 

(1. 거시-금융 현상) 금융 상황은 조건부 성장의 하위 5% 백분위수 성장위험 (GaR)이 그 중간값보다 더 큰 영향을 미친다는 것을 보여준다. 즉, 성장 위험이 금융 상황에 따라서 비대칭성을 보인다.

• 이때, 하위 꼬리의 계수 부호가 반전된다는 것을 보여준다. (즉, 평균 뿐만 아니라 하위 꼬리에도 영향을 미친다는 점이 특징이다). 또한 하위 꼬리 GaR이 금융 상황에 더 “민감 (sensitive)”하게 반응한다는 것을 보여준다.

 

(2. 기간 구조 분석) 금융 상황 (FCI) 영향에 따른 GDP 성장의 꼬리 위험은 기간 (horizon)마다 다른 양상을 보여준다. 초기 금융 조건이 느슨 (loose)해 질 때, GaR 즉, 성장 위험은 가까운 기간일수록 하락 리스크가 낮아지지만, 반대로 후기에는 점차 증가하게 된다. 이런 것을 intertemporal risk trade off라고 한다. 이는 Credit-to-GDP (GDP 대비 신용) 성장이 빠르게 이루어질 때 더 크게 증폭된다는 점을 확인할 수 있다.

• 초반에는 높은 GaR이 더 작은 하락 리스크를 보이지만, 중기에는 반전이 되어서 median과 비교했을 때, 하락 리스크가 더 낮은 GaR (더 큰 하락)을 보여준다는 것이 특징이다. 또한 느슨한 금융 환경과 높은 신용으로부터 예상되는 평균 성장은 기간이 지남에 따라 감소한다.
  • ** 이때, 예상 성장이 ‘하락 리스크가 더 커지는 비용을 상쇄’하기 위해 증가하지 않는 것으로 파악된다.Credit boom 지표는 FCI 가 느슨해지고, Credit-toGDP gorwht의 급격한 증가를 조합시킨 것인데, 주목할 것은 median 인지 하위 5th 인지에 따라서 움직임이 매우 달라진다는 것을 볼 수 있다.
• 원래는 계산이 매우 복잡하기 때문에, ‘조건부 성장(conditional growth)’과 ‘조건부 하락 (conditional downside risk)’ 사이에 강한 역상관 관계(inverse correlation)가 “dynamic” 동학적으로 무시되거나 성장이 변동성에 영향을 받지 않는다고 가정하고는 한다. 따라서 금융 조건에서 미래 하락 리스크를 과소평가할 수 있다는 것이다.

 

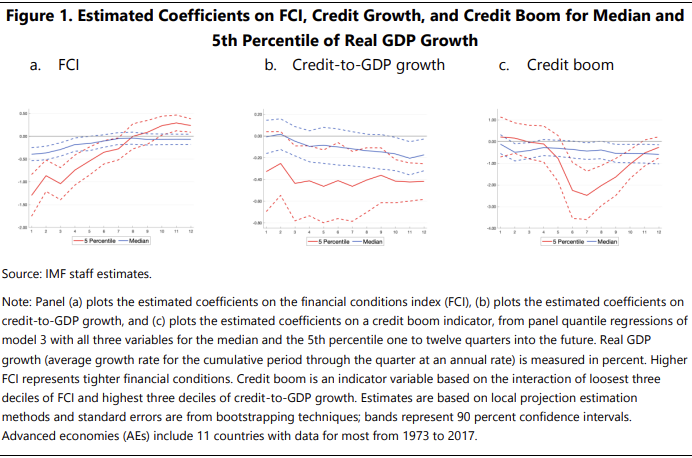
Credit boom 지표는 FCI 가 느슨해지고, Credit-toGDP gorwht의 급격한 증가를 조합시킨 것인데, 주목할 것은 median 인지 하위 5th 인지에 따라서 움직임이 매우 달라진다는 것을 볼 수 있다.

 

(3. 원인 분석) 도구 변수 (Instrument variable)를 사용해서 느슨한 금융 조건에서 미래 하락 리스크로의 관계가 인과적임을 제시할 수 있다. 이때, 결과는 거시-금융 모델에서 중기적으로 성장 하락 리스크를 체계적으로 고려하기 위해 높은 차수 모멘트의 내생성을 포함해야 함을 시사한다.

• GIV (granular instrumental variables; GIV)방법을 사용했을 때, 이는 단순히 내생적 편향 (endogeneity bias) 때문이 아님을 보여준다.
  • ** Gabaix and Koijen (2019)
  • 예상 부도 빈도 expected default frequency (EDF) index 를 사용하여, intertemporal 패턴에 대한 endogenous 편항을 제거
• 이때 거시건전성 정책 개입이 필요한 지, 개입되었다면 개혁이 잘 되었는지에 대해서도 생각해 볼 수 있다. 예를들어, 스트레스 테스트 시나리오의 심각도를 조정하거나, 경기 반전 주기에 따른 자본 버퍼 (a countercyclical capital buffe)를 설정 하거나 대역별 대비 비율 (borrower loan-to value), 대출 금액 대 소득 비율 (loan-to-income ratio) 비율 등을 보정하는 데 도움이 될 수 있다.
  • 이때, 은행 위기의 확률 (probability of a banking crisis) :불연속적 전환 → 연속적 전환 모형이 향후 필요함
• 또한 금융 안정 관련 리스크를 성장에 대한 리스크로 표현함으로써 통화정책에 더 잘 통합될 수 있다.

모형 및 추정은 위의 흐름에 맞게 정리해 두었다.

 

 

 

[모형 및 추정]

 

(경제 현상 및 메커니즘 분석) 1975년부터 2017년까지 11개 선진국의 실제 GDP 성장 분포와 금융 상황 간의 관계나 경향성에 대해서 연구한다. 기본 이론적 토대는 “**금융 마찰 (financial frictions)”**로 부터 나오는데, 비대칭 정보 (asymmetric information)와 규제 제약 (regulatory constra)과 같은 금융 마찰로 인해서 위험에 대한 가격이 낮을수록 오히려 금융 취약성이 쌓일 수 있으며, 위험 가격이 반전이 될 때, 급작스럽게 부정적인 파급 효과를 가져오고 그 크기가 더 클 수 있다는 것 (전이효과)을 보여준다.

• GDP 성장 분포에 대한 시간 변동성 (time-variation)은 초기 FC로부터 나온 “위험의 가격” 변화를 반영하며, 이 때에는 금융 기관의 신용 공급 (credit)을 통해 이루어 진다.

 

(모형) 모형은 금융 상황 (FCI), 신용 성장, 경제 상황, 인플레이션에 의존하는 성장 모델을 기반으로 panel quantile regression과 local projection을 사용한다. **성장 분포에 대한 기간 구조 (term structure for the distribution of forecasted growth)**를 생성하고, 특히 하위 5%에 초점을 맞추어 분석을 진행한다는 점에 주목해야 한다.

$$ Z_{t}=\theta_{t}^{y} Y_{t}+\theta_{t}^{f} f_{t}+v_{t} \\ \left[\begin{array}{l}Y_{t} \\ f_{t}\end{array}\right]=c_{t}+B_{t, 1}\left[\begin{array}{l}Y_{t-1} \\ f_{t-1}\end{array}\right]+\cdots+B_{t, p}\left[\begin{array}{l}Y_{t-p} \\ f_{t-p}\end{array}\right]+\varepsilon_{t} $$

• $Z_{t}$ 는 금융 변수의 벡터이고, $Y_{t}$는 거시경제 변수 (실질 GDP 성장과 CPI 인플레이션).
• $\theta_{t}^{y}$는 회귀 계수이고, $\theta_{t}^{f}$ 는 factor loading, $f_{t}$는 잠재적 요인으로 FCI로 해석

 

AE가 성장률이 낮으며, credit to GDP 는 더 높다.

 

(표 설명) 신용 성장과 FCI 각각 분포 상위 세게 범위에 있는 신용 붐이 있는 경우는 각 샘플에서 약 8%를 차지한다. 높은 FCI와 + 신용 성장이 어떻게 발전하고 성장하는지 관찰 가능하다.

 

Estimated FCI Coefficients with Interaction 예측 기간 동안 AEs와 EMEs의 5번째 백분위 수량 회귀에 대한 λ의 계수

 

(그림 해석) AEs의 λ에 대한 계수는 h=5부터 음수이며, 나머지 예측 기간 동안 음수로 유지되지만, 효과의 크기는 시간이 지남에 따라 완화한다. 계수 추정치는 초기 신용 붐의 한계 효과가 두 번째 해 내에 하향 리스크를 크게 증가시키는 것을 나타낸다(GaR 감소).

** 이때, 기대 성장의 분포를 변화시킬 수 있는 매크로금융 연계성과 일치

• 즉, 금융 조건에서 성장으로의 linkage가 단순히 공통 충격일 경우, 신용이나 신용 격차의 성장이 높아도 큰 비용을 예상하지 않을 것이다. 그러나, **높은 크레딧 성장 기간 (high credit growth periods)**에 중기에 추정된 더 높은 비용 (higher costs in the medium term)은 가까운 기간의 변동성 감소를 설명하는 내부적 위험 수용 채널 (endogenous risk-taking channel)과 일치한다고 할 수 있다.

 

(1) Growth at Risk

• 조건부 GDP 성장 분포를 기간 near-term (1Q~4Q), medium-term(5Q-12Q) 기간으로 나누어서 각각 살펴본다. **패널 분위수 회귀 (panel quantile regression)**를 활용한다.
  • 국가 i의 t부터 t+h까지의 연평균 GDP 성장률 $\Delta y_{i, t+h}$
  • 조건 변수 벡터 $x_{i, t}$
  • 조건 변수에는 FCI, GDP 성장률, 인플레이션, 크레딧 붐을 나타내는 더미 변수(높은 FCI와 높은 크레딧 성장률의 상호작용으로 정의) 및 상수가 포함된다.
• $$ \hat{\delta}_{\alpha} = \arg\min \sum_{t=1}^{T-h} \left( \alpha \cdot 1_{\Delta y_{i, t+h} > x_{i, t} \delta} \cdot \left| \Delta y_{i, t+h} - x_{i, t} \delta \right| + (1 - \alpha) \cdot 1_{\Delta y_{i, t+h} < x_{i, t} \delta} \cdot \left| \Delta y_{i, t+h} - x_{i, t} \right| \right) $$
• 국가 i의 $\Delta y_{i, t+h}$에 대한 패널 분위 회귀에서 회귀 기울기 $\delta_{\alpha}$는 오류의 분위 가중 평균의 절대값을 최소화하기 위해 선택한다.

 

$$ \hat{Q}_{\Delta y_{i, t+h} > x_{i, t}}(\alpha) = x_{i, t} \hat_{\delta}_{\alpha} $$

 

• 그런 다음 우리는 성장 위험(GaR)을 정의할 수 있다. 이는 미래 GDP 성장의 Value at Risk를 의미

$$ \Pr\left( \Delta y_{i, t+h} \leq GaR_{i, h}(\alpha | \Omega_{t}) \right) = \alpha  $$

• GaR은 주어진 확률 $\alpha$에 대한 예상 성장률로 정의
• 우리는 성장을 연간 평균 속도로 t에서 t+h까지 누적 성장률로 측정하여 단위를 더 쉽게 해석
• 이를 통해 다양한 시계에서 FCI 변화가 GDP 성장 분포에 미치는 평균 처리 효과 (estimated average treatment effect) 를 추정할 수 있게 됩니다.

 

(그림 해석) 하방 리스크 변동성 (5.2%)이 상방 리스크 변동성 (0.28%), 중위값 (1.4%) 보다 크다는 것을 확인할 수 있다.

• 백분위 분위 회귀의 추정값을 보고하고, 분위 회귀 추정값을 매핑하여 확률 밀도 함수를 표시한다. 이는 평균, 변동성, 비대칭도, 첨도 4가지 모멘트를 나타낸다.

$$ \text {skewed-t distribution } \\f(y ; \mu, \sigma, \theta, v)=\frac{2}{\sigma} d T\left(\frac{y-\mu}{\sigma} ; v\right) T\left(\theta \frac{y-\mu}{\sigma} \sqrt{\frac{v+1}{v+\frac{y-\mu}{\sigma}}} ; v+1\right) $$

 

 

Credit Boom 의 유무가 큰 차이를 유발한다는 점을 파악할 수 있다.

(그림 해석) 여기서 주목해야 할 점은 1) FCI 와 2) Credit Boom 의 유무, 3) Projection 기간 (horizon) 이다. 이때, Credit Boom 의 유무가 기간 사이에 큰 차이를 유발한다는 점을 파악할 수 있다. quantile regression 추정치를 skewed t-분포에 맞게 피팅하여 얻은 전체 확률 밀도 함수를 보는데, 두 가지 시점에서 초기 FCI (상위 1%) 및 신용 붐에 대한 조건부 성장 분포를 보여준다. 위의 그림은 AE (선진국)을 보여주는데, h=4에 대한 조건부 성장 분포는 왼쪽 꼬리에는 mass이 거의 없고, h=10에 대한 분포는 왼쪽에 많은 mass 를 가지고 있다.

반면 FCI는 높지만, 신용 붐이 없는 경우 h=4와 h=10일 때의 분포 변화는 덜 두드러지는 모습을 비교해 볼 수 있다.

 

---

(2) Condition for a Credit Boom

• 이제는 비선형성과 Amplication 효과를 포착하기 위해서 크레딧 붐 (Credit boom) 조건을 추가한다. 이는 금융 취약성 (financial vulnerabilities)이 높을 때, 위험 가격이 급증하는 negative 충격으로부터 비선형성이 발생할 수 있기 때문이고, 리스크 가격이 급격하게 상승하는 충격은 high credit 에 해당하면 더 큰 결과를 가져올 수 있다.
  • 이는 파산 (fire sales) 가능성이 높아지고 부채 과잉 (debt overhang)이 효율적인 가격 조절을 방해할 수 있다.
• 거시-금융 연결은 신용부채 대 GDP 비율의 성장을 과거 8분기 동안 측정한 것으로 정의한다. $\lambda_{i,t}$로 정의하고, t와 t+h 사이의 누적 성장을 이용한다.

$$ \lambda_{i, t}=\left\{\begin{array}{cc}1 & \text { if } \Delta \text { Credit-to-GDP and FCI each are in the top three deciles } \\0 & \text { else }\end{array}\right. $$

• $\lambda_{i, t}$는 두 변수인 FCI와 성장이 각각 분포의 상위 세 개 범주 (top three deciles)에 속할 때를 의미한다.
  • (a) 크레딧 성장이 높아질 때 (급격하게 뒤집혀 터질 때)
  • (b) FCIs가 아직 불황 긴장으로 남아있는 경우
  • ⇒ 위 두 경우를 배제하게 된다.

$\lambda_{i, t}$의 계수는 중기간 (medium term)에 더 음수가 되는데 이는 macro-finance linkage로 인해서 나타나는 output 성장에 나타나는 효과와 일치하게 된다.

• 높은 취약성 (vulnerability) 으로 인해 ‘높은 부채를 지닌 가계 및 기업' 및 ‘낮은 리스크 가격’ 이 결합되는 상황이기 때문에 오히려 미래에 금융 불안정성의 가능성이 증가할 수 있다.

 

• (메커니즘) 고부채 차입자들 (indebted borrowers)은 자산 가격이 하락할 때 순자산 가치가 하락하는 것 뿐만 아니라, 파산 가능성이 높아지고, 이는 “비선형적”으로 나타나 신용의 감소를 가져온다.
  • ** 따라서 이런 비선현성을 포착하는 것이 중요 ** 여기서 금융 조건 (FCI)를 리스크 가격 변화로 생각하면 된다.
  • 또한 순자산 가치의 급격한 하락과 촉매의 급격한 하락은 경기가 통화정책이나 금융 조건에 의해 통제될 수 없는 상황으로 이어질 수 있다. ⇒ 즉, 가까운 미래의 하락 리스크가 낮아질 것이지만 중장기적으로는 GDP에 대한 하락 리스크가 높아짐
  • ** 여기서 금융 조건 (FCI)를 리스크 가격 변화로 생각하면 된다. 

 

• (추정) 초기 평균 FCI 값에 따라 다음 네 가지 그룹에 대한 GaR 기간 구조 추정치를 보여줌 ⇒ 느슨한 FCI가 가까운 기간의 리스크를 낮추고 나중에 리스크를 높일 가능성이 있는지 평가
  • 상위 1% (매우 느슨한 (loose) 금융 조건)
  • 상위 백분위수 (느슨한 금융 조건)
  • 하위 백분위수 (매우 긴축적인 (tight) 금융 조건)
  • 중간 40% 및 credit boom지표인 $\lambda$가 0 또는 1인지 여부에 따라 분류

 

(위쪽 그림 해석) 1) 오른쪽 위와 왼쪽 위 그래프의 차이는 신용 붐이 있는지 없는지이고, 2) 각 그래프의 기간 구조는 리스크에 대한 intertemporal trade-off를 보여준다.

선진국 (AE)의 경우, 1그룹은 (느슨한 금융조건, 신용 붐) 은 가까운 기간 (h=1)에 대해서는 GaR 이 약 1%이지만, h=8 정도가 되면 -2% 밑으로 떨어지며 약 3%이상의 변동을 보여준다. 중간 범위의 초기 FCI**에 대한 추정 GaR은 처음에 상승하고, 중기에는 약 -0.5% 수준으로 안정화된다. 이때 중간 기간 구조는 상승하는 경사를 보여주기도 한다.

• ** 초기 FCI 값의 네 가운데 백분위수 (Mid 40)를 사용하여 “typical" 중간 조건을 대표하고, FCI가 높지 않고 낮지 않을 때의 예상 성장과 하락 리스크를 근사화

(아래쪽 그림 해석) 아래 그림은 다양한 FCI 그룹 간의 GaR 기간 구조의 차이를 비교하기 위해서 상위 1%와 중간 40% FCI 그룹 간의 GaR 그룹 간의 차이를 계산하고, 각 시점 h 에서 GaR 의 차이를 bootstrapping 하여 통계적 차이를 해석한다. 가까운 시점에는 양의 방향, 중간 지점에서는 음의 방향으로 통계적으로 유의한 모습을 보인다.

 

 

 

 

 

(기간 구조 (Term Structure)와 기간 상충 (trade off))

하위 5%의 하락은 더 높은 기대 성장(50% 지점)과 함께 나타날 수도 있으며, 이 경우 높은 성장과 높은 리스크의 대안적 해석이 가능하다. “초기 느슨한 금융 조건”과 “일반적인 금융 조건 간”의 추가 예상 성장과 하향 리스크 감소를 예측하여 기간 구조 상에서 평가할 수 있다.

 

(그림 해석) Top 10과 Mid 40 FCI 그룹에 대한 예상 중앙값 및 GaR 기간 구조를 보여준다. 먼저, 그림들의 공통점은 시간이 지나면서 각각 차이가 줄어든다는 것이다. 또한 모든 경우에서 상위 10%의 FCI는 모든 경우에서 중간 40%의 FCI에 비해 가까운 기간에 높은 GaR(하향 리스크가 낮음)를 가진다.

 

(그림 해석) 그림을 보면 둘다 하락을 하는 모습을 보이는데, 이는 &ldquo;하향 리스크&rdquo;의 하락 이 &ldquo;예상 중앙값 성장&rdquo;의 하락 보다 훨씬 가파르다 는 점을 알 수 있다. 특히 credit boom이 있는 경우 더욱 두드러진다 (오른쪽과 왼쪽 글미의 차이). 이는 credit boom에 대한 비용을 보여준다.

상충 관계에 대한 해석

• GaR과 확률 밀도 함수를 통해 높은 초기 FCI 그룹과 중간 정도의 초기 FCI 그룹 간의 기간 구조 차이가 통계적으로 다르다는 것을 보였다.
• 정책 결정 시, 미래 하향 리스크가 높아지는 중기 리스크와 관련하여 보다 낮은 하향 리스크를 포기할 가치가 있는지에 대한 고려가 중요한 것이다. 실제로 welfare 함수를 구체화 하지 않고 그저 trade-off 관계가 존재하는지 경험적으로 검증하는 것이다.