Measuring systemic financial stress and its risks for growth (Deep)

Measuring systemic financial stress and its risks for growth (2023)
저자 : Sulkhan Chavleishvili, Manfred Kremer
European Central Bank

 

“Money is a veil, but when the veil flutters, real output sputters.”

 

이 논문은 (1) Financial Stress Index를 시스템 위험 (system risk)에 기반해서 각 요소에 가중치를 두어 계산하고, 도출된 지수를 바탕으로 (2) economic growth 에 적용하는 논문이다.

 

이때 도출된 지표를 복합 시스템적 스트레스 지표(CISS)이라고 하기도 한다. 경제적 이론보다는 통계학적 프레임워크를 제안하는 논문이기 때문에, 금융 위험 지표가 어떻게 산출되는 지 technical 한 부분에 초점을 맞추어야 한다.

 

(1. 지표 측정) 재미 있는 점은 Financial stress index를 도출할 때, 금융 포트폴리오를 만들듯이 도출한다는 점이다. 즉, finance 이론에서 개별 자산의 위험에서 포트폴리오 위험을 계산하는 방식과 유사하다. CISS는 통화, 채권, 주식 및 외환 시장의 스트레스 증상을 포착하는 15개의 구성 요소를 통해 계산이 된다. 이를 기반으로 1) 극단성 (extremeness)과 2) 상호의존성 (co-dependence)을 측정하는 두 개의 행렬을 결합해서 행렬 연관 지수 (matrix association index)를 도출한다.

• 먼저 1) 극단성의 경우, 시스템 전체의 스트레스 (System-wide stress)는 지표 쌍 (paris)의 평균 교차 곱 (average cross-product)으로 계산하고, 2) 상호 의존성의 경우, 시간에 따라 변화하는 순위 상관관계 (rank correlation)에 따라 가중치가 부여되는데, 이때 상호 의존성은 전체 금융 시스템의 한 부분에서 다른 부분으로 전파되는 연쇄작용 (contagion)이나 파급효과 (spill over)를 포착한다는 점이 특징이다.

 

(2. 거시-금융 분석) real GDP 성장률에 대한 CISS의 단기 예측 능력을 평가하기 위해서, 1) 단일 방정식 (single equation) 및 2) quantile VAR (QVAR)을 적용하여, 실제 GFC기간이나 코로나 기간에 어떻게 침체 상황을 설명할 수 있는지 보여준다.

 

 

 

[1. 지표 측정]

Definition (Systemic Financial Stress)

Stress factors 인 $z_{i, t}$ 가 일반적으로 극도로 높은 (extremeness) 상태이며 서로가 강하게 상호 의존적인 (co-dependence) 상태이다.

 

위의 정의에 따르자면, "시스템적 금융 스트레스"는 높은 스트레스가 지역적으로 제한되어 다른 중요한 금융 시스템 부분에 영향을 주지 않는 경우를 배제해야 한다.

 

극도성과 상호 의존성은 NXN 크기의 제한된 실수값 행렬 $\mathcal{E}_{t}$ (상호 의존성 행렬)와 $\mathcal{C}_{t}$ (시스템적 위험 가중치)로 측정하며, 이를 결합한 시스템 금융 스트레스 지수 $\mathcal{S}_{t}$ 는 다음과 같이 정의한다.

 

$$ \mathcal{S}_{t} \equiv \frac{1}{N^{2}} \sum_{i=1}^{N} \sum_{j=1}^{N}\left(\mathcal{E}_{t}\right)_{i, j}\left(\mathcal{C}_{t}\right)_{i, j} $$

• Bootstrapping 을 이용해서, 시간별로 stress factor 가 상호 의존성을 가지지 않는다는 영가설을 통계적으로 검정
• 또한 만약 동등한 가중치를 가정하면 : $w_{i}=1 / N$

 

 

[데이터]

미국과 유럽의 주요 금융 시스템 부분에서 N=15 개의 Raw 스트레스 지표 $x_{i, t}$를 선택한다. 이러한 시장 구분 (segment)*는 주요 금융 자금 이동을 기준으로 다루는데, 이는 금융 중개기관을 통하거나, 단기 및 장기 증권 시장을 통해 궁극적으로는 최초 대출자에서 최종 차용자로 이동하는 자금의 주요 흐름을 의미하며 이로 구분이 된다.

• * (i) 비금융 기업의 주식 시장; (ii) 금융 기관의 주식 시장 (상장 은행 및 기타 거래 금융 업체); (iii) 자금 시장 (은행 간 시장, 상업용 증권 및 국채 시장); (iv) 국채 및 기업 채권 시장; (v) 외환 시장
• 모든 시장 구분 (segment)에는 향후 계산 시, 과거 변동성 측정치의 지수 가중 이동 평균 (EWMA; exponentiallyweighted moving average)이 적용 된다.

 

[통계학적 방법론]

Raw 스트레스 지표(index)는 $x_{i, t}$는 확률적 정적분 변환 (probability integral transform; PIT)을 통해 스트레스 요인 (factor) $z_{i,t}$ 로 바꿀 수 있다.

 

$$ z_{i, t}=\hat{F}\left(x_{i, t}\right):=\left\{\begin{array}{ll} \frac{1}{T_{0}-1} \sum_{s=1}^{T_{0}-1} \mathcal{I}\left(x_{i, s} \leq x_{i, t}\right), & \text { for } \quad t=1, \ldots, T_{0}-1 \\ \frac{1}{t} \sum_{s=1}^{t} \mathcal{I}\left(x_{i, s} \leq x_{i, t}\right), & \text { for } \quad t=T_{0}, \ldots, T \end{array}\right. $$

 

$\hat{F}\left(x_{i, t}\right)$는 지표 $x_{i, t}$의 cdf로 정의되며, $\mathcal{I}(x)$는 지시 함수이며, 적은 데이터 샘플에 대한 예상되는 통계적 문제를 해결하기 위해 PIT를 확장 데이터 샘플을 사용해서 재귀적 (recursive)으로 계산하게 된다.

 

(1) 극도성 (extreme)

 

스트레스 요인 (stress factor) 벡터 $z_{t}$는 극도성 (extreme)을 나타내는 자연스러운 척도이다. 다시 말하자면, 스트레스 지표 $x_{i, t}$가 역사적 최대치에 도달할 때 가장 극단값이 된다. (이 경우 $z_{i, t}=1$이 된다. )

그러나 이 논문에서 다루고자 하는 바는 “시스템 전체”의 극도성을 포착하려고 하는 것이기 때문에, 이를 위해 극도성을 비중심화되지 않은 모든 스트레스 요인인 $z_{i, t} \cdot z_{j, t}$의 교차 곱으로 정량화하고 대칭 행렬 $\mathcal{E}_{t}$로 나타낸다.

• 왜냐하면 교차 곱은 두 stress factor가 동시에 극단적인 상황에서 얼마나 높은 관계에 있느지를 측정해주기 때문이다.

 

$$ \mathcal{E}_{t}=z_{t} z_{t}^{\prime} $$

 

$(\mathcal{E}_{t})_{i, j}=(z_{t} z_{t}^{\prime})_{i, j} \in(0,1]$이므로, 극도성 행렬은 최대 시스템 스트레스에서 모든 요소가 1인 행렬 $J_{N}=\iota_{N} \iota_{N}^{\prime}$이 되며, 최소 스트레스에서는 모든 요소가 0인 행렬 $O_{N}=0_{N} 0_{N}^{\prime}$에 가까워진다.

 

 

서브프라임 모기지 때의 위기와 글로벌 금융 위기 후반에 값이 높아지는 모습을 보인다. b에서 파란선은 Ted 스프레드는 recursive하게 z점수로 표준화 되어 나타난 선이다. 빨간선은 전체 샘플 정보를 모든 시간에서 사용해서 변환한 결과이다.

 

(2) 상호 의존성 (Co-dependence)

 

여기서 상호 의존성을 비모수적 (non-parametrically)으로 계산한다. 이는 $N(N-1) / 2$ 개의 스트레스 팩터 쌍 간의 conditional rank correlation (Spearman의 $\rho$)인데, 여기서 랭크 상관 관계는 두 스트레스 팩터가 어떤 시간에 비슷하게 높거나 낮은 지를 나타낸다.

• 예를 들어, 두 스트레스 요인이 함께 cdf의 상단 범위로 움직인다면, 동일한 조건 하에서 금융 스트레스가 보다 확산되어 체계적인 위험이 증가할 가능성이 높다. 그러나 이들이 같이 움직이지 않는다면, 이 위험은 낮아진다.

 

스트레스 요인는 raw 데이터의 1) 자기상관 (autocorrelation) 및 2) 이분산성 (heteroskedasticity)의 특성을 그대로 가지기 때문에 두 스트레스 팩터 $z_{i, t}$와 $z_{j, t}$ 간의 랭크 상관관계 (Rank Correlation)를 시간에 따라 조건부 시계열 기대값 $\rho_{i, j, t}:=E_{t}\left[\rho_{i, j, t+1} \mid z_{i, t-k}, z_{j, t-k}, \rho_{i, j, 0}\right]$로 추정할 수 있다.

• 조건부 기대값은 다변량 GARCH 문헌을 따르는 자기회귀적 지수가중이동평균(EWMA)으로 비모수적으로 모델링
• 랭크 상관계수를 통해 중심성 척도에 대해 정의
  • 스피어먼 랭크 상관계수는 두 변수의 순위를 사용하여 계산 ⇒ 이는 변수의 값 자체보다는 순위에 초점을 맞추기 때문에 분포의 형태나 이상치에 덜 민감
  • 우리는 중심성 척도로 모집단 중앙값 0.5를 취하고, 이에 따라 중심화된 스트레스 팩터 벡터를 $\tilde{z}_{t}=\left(z_{t}-\iota_{N} \cdot 0.5\right)$로 정의 ⇒ 중앙값은 데이터 집합의 중심적인 값으로, 데이터를 크기순으로 나열했을 때 가운데 위치하는 값을 의미하며, 데이터의 중앙을 기준으로 상대적인 위치를 파악
• EWMA 필터는 중심화된 스트레스 요인 $\tilde{z}_{t}$의 분산-공분산 행렬 $H_{t}$에서 실행
  • 여기서 매개변수 $\lambda=0.85$로 둔다.

$$ H_{t}=\lambda H_{t-1}+(1-\lambda) \tilde{z}{t} \tilde{z}{t} $$

 

상관관계 행렬 $R_{t}$의 요소 $\rho_{i, j, t}$는 중심화된 스트레스 요인 $\tilde{z}_{t}$의 요소 $h_{i, j, t}$에서 다음과 같이 계산된다. $\rho_{i, j, t}=h_{i, j, t} / \sqrt{h_{i, i, t} h_{j, j, t}$

•  스피어먼의 $\rho$행렬 $R_{t}$은 시스템 위험 가중치 행렬

 

 

글로벌 금융위기(GFC) 및 COVID-19 위기 전후의 금융 안정성 상황을 나타내는 네 시기에 대한 "극도성"과 "상관 행렬"을 시각화하는 등고선 도표 (contour plots)이다. 각 패널에서 주대각선 아래는 극도성, 위는 상관관계가 나타난다.

(그림 해석) 왼쪽은 위기 직전, 오른쪽은 위기 직후를 나타내고, 위는 글로벌 금융위기 아래는 코로나 시기를 보여준다. 그림에서도 한눈에 보이다시피, 오른쪽은 극단적으로 빨간색이 되어 있어 얼마나 금융 스트레스 수준이 높았다. 특히 코로나 시기에는 짧은 시간 안에 얼마나 금융 스트레스가 증가했는지를 확인할 수 있다. 십자 모양 (cross)으로 나타난 곳은 “nonfinancial corporations-price-book ratio” 비율을 나타내는 곳인데 여기만 크게 증가하지 않음을 확인할 수 있다.

 

이제 위 두 구성 요소를 합치는 일이 남았다.

 

(3) 종합 지표 (Composite Indicator)

 

이제 모든 구성 요소를 갖춘 상태에에서는 CISS를 쉽게 계산할 수 있습니다. 행렬 연관 지수 $\mathcal{S}_{t}$ 를 기반해서 아래와 같이 계산을 한다.

 

$$ \operatorname{CISS}_{t}=\frac{1}{N^{2}} \sum_{i=1}^{N} \sum_{j=1}^{N}\left(z_{t} z_{t}^{\prime}\right)_{i, j}\left(R_{t}\right)_{i, j} $$

 

$R_{t}$가 주 대각선에만 1이 있는데, 각 (제곱된) 스트레스 요인은 단위 체계적 위험 가중치로 이 척도화된 항목별 곱의 합에 들어가며, 교차 곱의 위험 가중치 (즉, $R_{t}$의 상·하대각 요소)는 일반적으로 1보다 작아지며 스트레스가 지속적으로 높거나 낮을 경우에만 1에 가까워진다.

• ** 이 식은 금융 분야에서 잘 알려져 있으며, 동등한 포트폴리오 가중치을 갖는 자산의 수익률 분산(위험)을 어떻게 계산하는지를 나타낸다는 것과 유사

 

CISS는 동등한 포트폴리오 가중치 w와 스트레스 요인 $z_{t}$의 요소별 곱셈 ($\circ$) 을 이용한 이차 형태로도 표현할 수 있다.

$$ \operatorname{CISS}_{t}=\left(w \circ z_{t}\right)^{\prime} R_{t}\left(w \circ z_{t}\right) $$

 

(그림 해석) 1973년 1월부터 미국과 1980년 1월부터 유럽 지역의 CISS를 보여준다. 지표의 주목할만한 뾰족한 꼭대기 대부분은 잘 알려진 글로벌 위기 사건과 연관시킬 수 있다. 이 사건에는 1987년의 주식 시장 붕괴, 1998년의 LTCM 파산, 2001년의 9/11 테러, 2007년의 서브프라임 모기지 , 2008년의 리만 브라더스 파산 및 최근의 COVID-19 위기 등이 있다. 그러나 1979년부터 1982년까지 폴 볼커 의장의 연준 통화 긴축 정책과 관련된 미국 내부적 충격, 1980년대 초에 발생한 은행 (savings and loan crisis) 위기, 1992년의 유럽 환율 기구 (European Exchange Rate Mechanis; ERM) 위기 및 2011년과 2012년의 유럽 지역 국채 위기 (sovereign debt crisi)와 같이 더 지역적 충격을 반영하는 경우도 있다.

 

(4) 분해 (Decomposition)

 

CISS 분해는 모든 시점에서 모든 스트레스 팩터가 완벽하게 상관된다는 가정에서부터 시작된다. 이 경우, 상관 행렬 $R_{t}$은 전부 1인 행렬 $J_{N}$이 되어 중복되어, CISS 공식이 다음과 같이 단순화할 수 있다.

 

$$ \begin{aligned} \operatorname{CISS}_{t} &=\left(w \circ z_{t}\right)^{\prime} J_{N}\left(w \circ z_{t}\right)=\left(w \circ z_{t}\right)^{\prime}\left(w \circ z_{t}\right) \\ &=\left(\sum_{i=1}^{N} w_{i} \cdot z_{i, t}\right)^{2}=\bar{z}_{t}^{2} \end{aligned} $$

 

따라서 완벽한 상관관계의 경우, 스트레스 팩터들의 동일한 가중 평균인 $\bar{z}_{t}^{2}$가 CISS의 상한으로 나타나게 되며, 체계적 위기에서 스트레스가 전반적으로 높은 경우, CISS가 $\bar{z}_{t}^{2}$로 수렴함을 의미하기도 한다.

반대로 상호 상관관계가 일반적으로 더 약할 때, CISS는 단순 평균 FSI와 더 큰 차이를 보이게 됩니다. 이에 따라 CISS와 $\bar{z}_{t}^{2}$의 차이를 상관관계 할인(correlation discount)이라고 부르고 이를 CISS의 분해에 사용한다.

$$ \mathrm{CISS}_{t}=\sum_{i=1}^{N} \frac{\bar{z}_{t}}{N} z_{i, t}-\left(\frac{1}{N^{2}} \sum_{i=1}^{N} \sum_{j=1}^{N} z_{i, t} z_{j, t}\left(1-\rho_{i, j, t}\right)\right) $$

 

위 식의 첫 번째 항은 간단히 $\bar{z}_{t}^{2}$ 을 N개의 스트레스 팩터 기여로 분해한 것이고, 두 번째 항은 상관관계 할인이라고 할 수 있다.

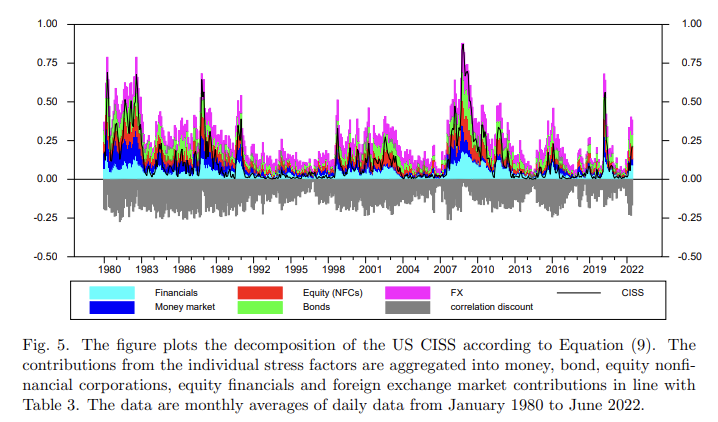
스트레스 요인을 다섯 개의 시장 구분에서 집계한 상태로, \bar{z}_{t}^2 의 분해

 

 

(그림 해석) CISS와 누적된 기여들이 GFC 동안 근접하게 일치하는 것을 확인할 수 있으며, 상관관계 할인이 0에 가까워진다. 더 중요한 것은 상관관계 할인의 패턴이 (회색 음영 영역) CISS의 주요 장점을 명확하게 보여준다. 이것은 상승한 스트레스가 보다 지역적이고 시장 특정 이벤트인 경우에 더 적은 가중치를 부여하여 실제로 널리 퍼진 금융 스트레스 (체계적 위기)의 에피소드를 더 잘 식별하도록 도와주기도 한다.

• 1990년대 후반과 2000년대 초의 닷컴 버블은 대부분 체계적이지 않은 스트레스 에피소드의 좋은 예라고 할 수 있다.

---

 

 

 

[거시-금융 분석]

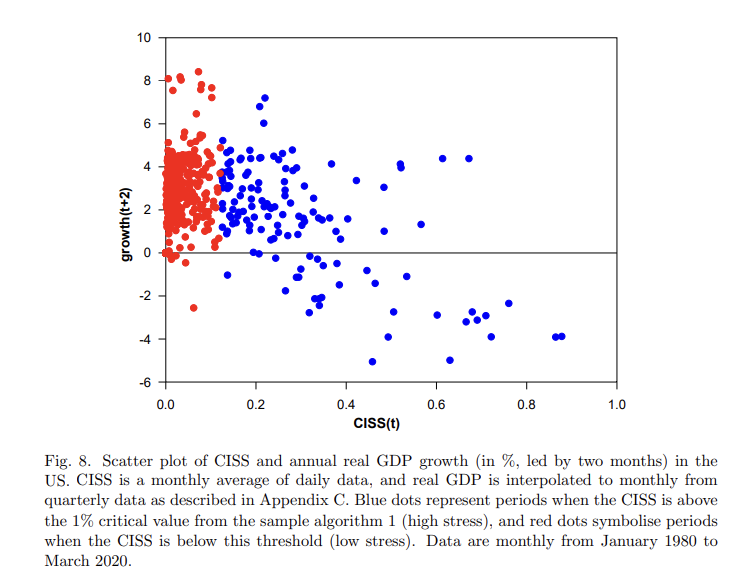
(하방 리스크) 체계적 금융 스트레스의 실제 영향을 조사하며, 특히 이러한 영향의 비대칭성에 중점을 둔다. 조건부 경제성장 분포의 하위 꼬리에서 금융 스트레스 또는 금융 조건 지표의 강력한 단기 예측력을 찾아낸다. 이론적 근거로 여러 메커니즘을 반영할 수 있는데, 예를 들자면, 급격하게 증가하는 금융 마찰과 불확실성은 자산 매각 및 신용 제한이 binding되어 가는 상황에서 증폭될 수 있다는 점이 “비대칭성”을 설명하는 가장 유명한 설명이다.

먼저 1) 단기적인 하방 리스크를 예측 (Direct growth forecasting)하고, 2) QVAR을 이용해서 경제 활동 측정값의 “동적” 영향도 평가한다.

 

(Direct growth forecasting) $\Delta y_{t+h}$는 t부터 월 t+h까지의 연환산 (annualised) real GDP 성장률을 나타내며, $\theta$는 회귀 분위를 나타낸다. $\epsilon_{t+h}^{\theta}$는 예측 오차를 의미하고. 3개월 예측 기간 ($h=3$)에 대한 식을 다음과 같이 나타낸다.

$$ \Delta y_{t+h}=\beta_{0}^{\theta}+\beta_{1}^{\theta} C_{I S S_{t}}+\beta_{2}^{\theta} P M I_{t}+\beta_{3}^{\theta} \Delta y_{t-1}+\epsilon_{t+h}^{\theta} $$

 

 

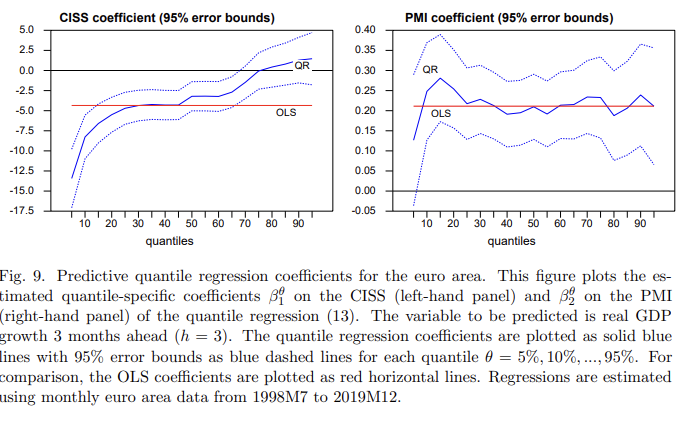
(그림 해석) CISS의 예측 계수는 회귀 분위의 최하위 (5%)에서 최상위 (95%)까지 그래프로 나타내었을 때, 뚜렷한 비대칭 패턴을 보인다. 성장 분포의 하위 꼬리에서 CISS의 예측력은 강하며, 5% 분위에서는 약 -13의 음수 계수를 갖는 모습도 볼 수 있다.

 

PMI에 대한 분위 회귀 계수는 성장 분포 전체에 걸쳐 안정적이며, OLS 추정치인 약 0.2에 가깝다. PMI와 미래 실질 GDP 성장과의 관계는 본질적으로 선형적 (linear)이라는 것을 확인할 수 있다. 또한 시스템적 스트레스가 경제 성장에 주로 영향을 미치는 것이 경기가 나쁜 상태에서 주로 발생한다는 예상과 부합한다.

 

(QVAR) QVAR에는 monthly frequency 로 측정된 세 가지 종속 변수 (CISS, PMI , real GDP growth) 가 포함되며, 변수 간의 상호 관계를 탐색하기 위해 구조적 충격을 식별하는 데 촐레스키 분해 (cholesky decomposition)를 활용한다.

$$ y_{t}=\phi^{\theta}+\sum_{l=1}^{2} \Phi_{l}^{\theta} y_{t-j}+\Gamma^{\theta} y_{t}+\varepsilon_{t}^{\theta} $$

 

• 여기서 $y_{t}$는 CISS, PMI 및 실제 GDP 성장과 같은 종속 변수들을 순서대로 모아 놓은 벡터
• $\phi^{\theta}$는 주어진 특정 분위수 (quantile) $\theta \in (0, 1)$에 대한 절편
• $\Phi_{l}^{\theta}$는 j 까지의 시차를 나타내는 계수 (lag coefficient) 를 2개의 quantile-specific 한 $3 \times 3$ 행렬
• $\Gamma^{\theta}$는 주 대각선이 0으로 이루어져 있는 하삼각 행렬 (lower triangular matrix)인데, 동시 계수 (contemporaneous coefficients)가 식별

 

여기서 $\mathcal{F}{1, t}=\left(y{t-1}^{\prime}, y_{t-2}^{\prime}\right)^{\prime}$ 및 $\mathcal{F}{i, t}=\left(\mathcal{F}{i-1, t}^{\prime}, y_{i-1, t}\right)^{\prime}$ 을 i=2,3에서의 recursive information set 이라고 정의해 볼 수 있다. 이때, “조건부 분위수 함수 (Conditional quantile function)”는 변수들 간의 관계를 전체 조건부 분포에서 설명하는 데 사용할 수 있으며, 특정 제약 (conditional quantile restriction)을 통해 얻을 수 있다.

 

$$ \begin{array}{l} \operatorname{Pr}\left(y_{i, t}<Q_{y_{i, t}}\left(\theta \mid \mathcal{F}{i, t}\right))=\theta, \quad i=1,2,3\right.\\ \Leftarrow Q{y_{t}}=\phi^{\theta}+\sum_{l=1}^{2} \Phi_{l}^{\theta} y_{t-j}+\Gamma^{\theta} y_{t} \end{array} $$

 

이 회귀 (Regression)는 Koenker 및 Bassett (1978)의 numerica 문제를 해결하는 것과 같다고 생각하면 된다.

$$ \hat{\beta}{i}(\theta)=\arg \min {\beta \in \mathbb{R}^{d}} \sum_{t=3}^{T} \rho_{\theta}\left(y_{i, t}-Q_{y_{i, t}}\left(\theta \mid \mathcal{F}_{i, t}\right)\right), $$

• 여기서 $\beta_{i}(\theta)=\left(\left(\phi^{\theta}\right){i},\left(\Phi{1}^{\theta}\right){i, \cdot}, \ldots,\left(\Phi{p}^{\theta}\right){i, .},\left(\Gamma^{\theta}\right){i, .}\right)^{\prime}$는 변수 i에 대한 방정식의 d개의 파라미터를 나타내는 벡터
• $\rho_{\theta}(u)=u(\theta-I(u<0))$는 비대칭 손실 함수 (asymmetric loss function)를 나타내며, $I(u<0)$는 지시 함수

 

 

[분석 결과]

다음으로는, 이 QVAR 모델 결과를 QIRF로 요약해서 보여줄 수 있다. 즉, QIRF는 모델 변수 간의 직접 및 간접적인 (direct and indirect), 지연 및 동시적인 (Lagged and contemporaneous) 상태와 상호작용 (state-dependent interactions)을 압축해서 보여준다.

** Chavleishvili 및 Manganelli (2019)의 시뮬레이션 알고리즘을 사용하여 QIRF를 계산

특히, QIRF의 개념은 일반적인 linear VAR의 IRF와 달리 조건부 평균 효과만을 추정하는 것과는 다르다. 한 변수의 조건부 분포의 한 특정 부분이, (변수들 중 하나가 예측되지 않게 변화했을 때) 다른 부분과 어떻게 다르게 반응하는 지를 보여준다. 시간 범위 $h \geq 1$에 대해 QIRF는 다음과 같이 정의할 수 있다.

 

$$ Q_{y_{t+h}}\left(\theta \mid \mathcal{F}{t+1}, \delta{i}\right) - Q_{y_{t+h}}\left(\theta \mid \mathcal{F}_{t+1}\right), \quad \theta \in (0,1)^{3} $$

 

여기서 $\delta_{i}$는 특정한 구조적 충격 (certain structural shock)이 발생한 후의 변수 $y_{i, t+1}$ 값을 (i=1,2,3)나타낸다.

각 변수가 번갈아가며, 해당 변수의 unconditional empirical distribution의 중앙값에서 표준 편차가 1인 역 충격 (adverse shock)을 주는 quantile impulse response function(QIRF)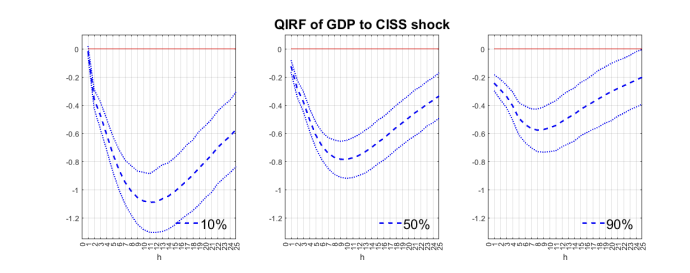

주목해야할 3행 3열 부분

(그림 해석) CISS, PMI 및 real GDP growth에 대해, 해당 충격 이후의 값인 $\delta_{i}$는 $\delta=(0.2196,47.3143,-0.9631)$으로 설정하며,. QIRF는 시간 범위 $h=1, \ldots, 24$ 와 3가지 분위수 $\theta \in(0.1,0.5,0.9)$에 대해 계산한다.

• 첫 번째 열과 행의 QIRF는 CISS의 충격 (impulse)나 반응 (response)과 관련된 것으로, 이러한 QIRF는 몇 가지 뚜렷한 비대칭성 (asymmetry)을 보여준다. 특히 흥미로운 점은 성장에 대한 CISS 충격의 효과 (3행 3열 그림)가 성장 분포의 $10%$ 분위수에서 중앙값 및 $90%$ 분위수와 비교하여 훨씬 더 강하게 나타난다는 것을 알 수 있다
  • $+0.18$의 CISS shock은 $10%$ 분위수의 성장 분포에서 약 1년 정도의 기간 동안 연간 실제 GDP 성장률을 최대 $1.1%$ 감소 시키며, 중앙값과 $90%$ 분위수에서는 각각 $-0.8%$ 및 $-0.5%$로 나타난다.
• 또한 거시-금융 연결 (linkage)에서 발견되는 비대칭성과 달리, 그냥 경제 활동을 보여주는 두 변수 간의 QIRF는 선형적인 모습을 보인다는 점도 특징이다. 즉, “금융 연결”이 비대칭의 요인이라는 것을 역으로 보여주는 셈이다.

이제 QVAR을 사용하여 CISS가 시스템적 금융 위기의 지표로서 얼마나 잘 작동하는 지를 평가해야 한다. 이를 위해 2008 GFC와 COVID-19 시기, 두 가지 경제 위기 상황을 다루는 대조적 시나리오 (counterfactual scenarios)를 실행해서 살펴본다.

(그림 설명) 예측 기간은 24개월로 두고, 두 기간에는 세 가지 다른 시나리오로 계산이 된다. 우선 실제 real GDP growth는 파란색 실선이다.

1. unconditional한 예측으로, 어떤 충격에도 노출되지 않는다고 가정 (하늘색 점선)
2. CISS를 예측 기간 동안 그 실현 경로를 따르도록 제한하며, CISS 분위수에 대해 일련의 구조적 충격을 암시적으로 가정해서 제한이 충족되도록 한다. 이 시나리오에서는 1% ~ 99% 까지 조건부 분위수를 포함하는 팬 차트를 그린다. (검정색 점선)
3. 예측이 CISS와 PMI의 실현 경로를 따르도록 고정시키고, 중앙값 조건부 성장 예측을 그린다. (빨간색 점선)

⇒ 즉, 2) 와 3)을 통해서 real GDP 성장 예측에 대한 “책임”이 금융 스트레스로부터 오는 것 (CISS)인지, 비즈니스의 심리적 충격 (PMI)인 것인지 대략적으로 판단해 볼 수 있다.

• (그림 해석) 두 위기 상황에서 모두 경제 활동이 전례 없는 심각성과 속도로 붕괴되었는데, 주목할 점은 “금융 스트레스”가 경제 하락의 주요 원인이었던 것은 GFC의 경우에만 해당되며 팬데믹의 경우는 해당되지 않는다고 분석해볼 수 있다.