Growth at Risk From Climate Change

 
관심을 ‘가져야 할’ 주제인 ‘climate change’ 관점에서 나의 관심 주제인 growht at risk를 살펴보고자 한다. 인류를 초월한 행성의 경제학..! 🪐
 
다만, 이번 페이퍼 목적은 climate 보다는, 아이디어와 방법론에 조금 더 초점을 맞추어 보았다.

• 어떤 데이터로 growht at risk를 어떻게 살펴볼 것인지, 내가 원하는 주제로 호환해서 생각해 보고자 했고, 데이터를 어떤 방식으로 살펴보아도 robustness 한지 보여주는 방법에 대한 중요성도 다시 잡아보고자 했다는 점이다.
• “왜 평균이 아닌, 위험의 분포를 보지?” 이거는 내가 가지고 있는 연구 주제인 credit cycle과도 연결을 지을 수 있다. 중심적인 영향이 아니고, 경제 활동의 ‘변동’성이나 ‘하향 위험’이 “잠재적으로 증가”한다는 것이다.
  • 즉, 더 따뜻해지는 우리 행성이나 기후의 “다른 측면과 관련된” 경제 침체에 대한 심각한 변화 정도와 관련있다. (간접적인 영향이네…) 더 높아지는 평균 온도는 경제의 생산성 저하, 무역이나 생산 네트워크의 혼란을 가져오고, 이것들이 경제 침체 요인의 위험을 증가시킬 수 있는 것이 문제이다.
  • 기온이 성장에 미치는 위험 증대에 매우 강한 영향을 보이는데, 이를 어떻게 볼 것이냐? GDP 성장의 하한 분위수로 측정된 ‘하향 리스크’는 중심 경향에 비해 훨씬 더 많이 영향을 받는다는 것을 통해 알 수 있다.
    • 기온이 growth rate 분포의 하한 10th에 미치는 영향은 분포의 median에 비해 50 퍼센트 이상 크다는 점 !

 
 
기후의 변화가 어떻게 경제 활동 (economic gorwth)에 대한 위험에 영향을 미칠까? 이를 설명하는 방법론으로는, 기후 변화가 경제 활동에 더 심한 수축을 가져올 가능성이 더 높은지 여부를 확인하기 위해 ‘성장과 온도(temperature)’를 연결하는 분위수 회귀(quantile regressions)를 사용한다. 온도가 경제 성장의 하방 리스크 (downside risk)에 미치는 영향은 모든 specification에 대해서 크고 견고 (robust)하다. 즉, 기후 변화로 인한 경제 성장의 리스크가 크다는 것을 보여준다. 
 
 

제목 : Growth at Risk From Climate Change
저자 : Michael T. Kiley (2021)
출처 : FEDS

 
 
[데이터]
온도 (temperature) 데이터는 Terrestrial Air Temperature and Precipitation (1900~2006)에서 가져오고, 국가 수준에서 인구수로 가중치를 주었다. 경제 성장 데이터(real GDP per capita)는, World Bank’s World Development Indicators 에서 가져와서 percentage change (annual basis)에 초점을 둔다. (국가는 총 124개 국을 포함)
 
(기초 데이터) 데이터로 covered 된 분석으로, 50년 동안 세계가 더 따뜻해졌으며, 평균 온도는 1950년대부터 세기 전환까지 약 1°C 상승했다고 한다. 2) real GDP 1인당과 온도 간에는 음의 횡단면 상관 관계를 보인다. (즉, 더 더운 나라일수록 더 가난한 경향)

• ** 온도와 소득 간의 인과 관계를 어떻게 식별할 것인지에 대한 논쟁 (Sachs 및 Warner, 1997; Gallup, Sachs 및 Mellinger, 1999; Acemoglu, Johnson 및 Robinson, 2002; Sachs, 2003)
• * 온도와 소득 간의 인과 관계를 어떻게 식별할 것인지에 대한 문제와도 맞닿아 있다.

 

부유한 국가가 가난한 국가보다 더 낮은 기온 (level)을 가진다는 점을 알 수 있다. 또한 중요하게 보아야 할 점은 GDP의 percent change이다. 왜냐하면, 이번 연구의 목적이 ‘변동’을 보는 것이기 때문이다.

• 서구 유럽 및 그 관련국과 세계의 다른 지역 간의 평균 온도 '차이'가 명확
• 국가별로 연간 실질 GDP 변화는 변동폭이 상당하다고 보여지며, 국가 내 변동성은 전체 표본의 변동성과 유사

온도의 변동은 대부분 국가 간에 나타나며, 국가 내 표준편차 (SD)가 국가 간 차이에 비해서는 작다.
 
 
 
 
[방법론]
(1. Quantile Regression) 국가 내 실질 GDP 1인당 변화 분포에 중점을 둔다. 국가 j의 기간 t 내에서 시간 t 정보 I$(t)$에 조건부를 걸고, 국가 j의 실질 GDP 1인당 변화의 ‘누적 분포 함수’를 $G_j(Δy(t) | I(t))$로 표시할 때, Z 번째 조건부 백분위수는 다음 식으로 쓴다.
 
$$ Q_j^0.Z(t) = G_j^{(-1)}(0.Z | I(t)) = {Δy(t): G(Δy(t) | I(t)) ≥ 0.Z} $$
 
 
(의미) ‘실질 GDP 1인당 growth rate’의 10th 조건부 백분위수는 t 기간의 실질 GDP 1인당 growth rate의 가장 작은 값으로, 해당 값보다 작을 확률이 10% 이상이라는 말임
 
(메커니즘) 이때, 1) 온난화로 인한 온도 상승이 ⇒ 경제 활동에 부정적인 영향 (예를 들면, 경제 생산의 급격한 감소)을 미칠 수 있음을 강조한다. 또한, 2) 기후 변화와 관련된 평균 온도의 증가는 경제 성장의 변동성을 증가시킬 수 있으며, 이는 경제 성장의 연간 변동에서 하향 치우침으로 이어질 수 있다.
 
 
(2. Equation - Central tendency) 실질 GDP 1인당 변화와 온도 분포 사이의 방정식은 다음과 같다.
 
$$ Δy(t, j) = a_j + A_D D +\underbrace{ F(T(t, j))}_{robust \ check 를\ 위한 \ 여러 \ 방법론들} $$
 

• $Δy(t, j)$는 국가 j의 기간 t 내에서의 실질 GDP 1인당 변화
• $T(t, j)$ 는 국가 j의 기간 t 내에서의 평균 온도
• 분위 회귀분석에는 국가별 fixed effects $(a_j)$ 및 quadratic country‐specific time trends 나 연도 더미변수 (dummy) ($A_D D$)도 포함

 
이때, 서구 유럽 및 미국, 라틴 아메리카(브라질), 아프리카 아래 사하라 지역(나이지리아) 및 동남 아시아(인도)를 대표적인 국가로 보고, 결과 reporting한다.
 
 

(표 해석) 경제 성장의 불이익적인 영향은, (1) 더운 국가 (열대 국가) (1열 및 2열, 상단 패널) . (2) 가난한 국가 (3열 및 4열)에 국한되는 경향이 있다. ($a_{1,1}$를 집중해서 보자.) 또한, 성장의 central tendency는 연평균 온도가 1°C 증가할 때 국가별 경제 성장이 약 1% 포인트 감소한다는 점도 같이 확인해 볼 수 있다.

• 평균 온도가 25.64°C인 "더운 나라 (예: 75th 백분위수) & 가난한 나라"를 고려할 때, 온도가 성장에 미치는 영향은 명확하게 나타남
• 이때, 평균 온도 25.64°C는 1986-2005년 사이의 연도별 평균 온도에서 75th 백분위수에 해당하며, 이 기간 동안 평균 연간 온도가 이 값 이상인 국가의 25%가 있음을 의미함

 
 
 
(3. Robustness Check) 결과의 robustness 을 보장하기 위해 $F(T(t, j))$에 대한 여러 선택 옵션을 살펴볼 수 있다.

(case 1) Quadratic in temperature

 
$$ F(T(t, j))=a_{1,0} T(t, j)+a_{1,1} T(t, j)^{2} $$
 
데이터가 ‘성장’과 ‘평균 온도’ 사이의 관계를 유연하게 적합하도록 허용한다.

• ** 즉, 초기 "추운 (차가운)" 기온을 가진 국가의 경우, 온도가 증가함에 따라 더 성장이 증가하고, 초기 "더운" 온도를 가진 국가의 경우 온도가 감소

 

(case 2) Quadratic in temperature with temperature change interactions

 
$$ F(T(t, j))=a_{1,0} T(t, j)+a_{1,1} T(t, j)^{2}+a_{2,0} \Delta T(t, j)+a_{2,1} T(t, j) \Delta T(t, j) $$
 
이렇게 모델링을 하면, 기후 변화와 관련되지 않을 가능성이 있는 단기적인 온도 증가로 인한 영향을 제거할 수 있다.
 

(case3) Linear & low‐income effect of Temperature:

 
$$ F(T(t, j))=a_{1,0} T(t, j)+a_{1,1} T(t, j) I_{\text {low income }} $$
 
여기서는, 온도 수준에 따라 영향을 구분하지 않지만, 저소득 국가와 고소득 국가 간에 미치는 영향을 구분한다. 즉, 가난한" 국가와 "부유한" 국가 사이에서 온도의 효과를 다르게 본다.

각 10분위에서 90분위까지의 각 10th에 대한 분위 회귀 결과를 reporting

위에서 작성한 (1)~(3) 식 을 적용해서 본 식은 다음과 같다. (1)은 10th로 하방 위험이라고 보면 된다.
 
(상단행) 우선 가장 상단의 행을 보면, 성장의 하향리스크 (10분위수)가 온도와 더 강하게 연관되어 있다는 점을 알 수 있다.

• 온도가 1°C 증가할 때 10분위의 경제 성장에 미치는 주효과는 -1.9%이며 중앙값에는 -1.3%정도 된다. 10th(1.534)에 대한 영향은 90th(0.673)에 비해서 두 배로 더 높음
• 성장의 하향리스크 (10분위수)가 온도와 더 강하게 연관되어 있다는 점을 알 수 있다.

 
(중간행) 단기적인 온도 ($\Delta$)의 변화를 넣는 것은 ($a_{10}+2 \cdot a_{11} \cdot 25.64$)를 보면 ‘온도와 성장의 관계’를 약화시키고 특히 median 보다 상위 분위수에서 더욱 두드러진다. 중위수를 기준으로 통계적 유의성도 분위수가 높아지면서 점차 감소한다는 것을 확인할 수 있다.
 
(마지막행) 또한, (3) ‘소득 수준 간 나라를 구별’하는 것은 주된 결과에 영향을 미치지 않는다. 10th quantile과 온도 사이의 연결을 통한 추정은 median 대한 영향보다 약 50% 더 크게 나타나고, quadratic의 경우에도 10th quantile에 대한 영향은 90th quantile에 대한 영향의 3배로 커진다.

• 더 따뜻한 온도와 관련된 성장의 하향 리스크가 급격히 증가함을 재차 보여주고 통계적 유의성은 quadratic 보다 level에서 유의미하게 나타난다는 점도 확인 가능하다.

 
이런 것들은 기후 변화와 관련된 온도 상승이 경제 활동에 부정적인 영향을 미칠 수 있는 정도를 과소 평가할 수 있다는 것을 보여주기도 한다. 또한, 짧은 기간 동안 도출된 효과가 기후 변화와 관련된 온도 변화로 확장되지 않을 수 있으므로 주의를 해야 한다.
 
 
이제는 위의 분위 회귀를 아래의 식에 넣으면
 
$$ Δy(t, j) = a_j + A_D D +\underbrace{ F(T(t, j))}_{robust \ check 를\ 위한 \ 여러 \ 방법론들} $$
 
경제 성장 분포에 미치는 영향은 서양 유럽 및 미국 (미국), 라틴 아메리카 (브라질), 아프리카 이남 지역 (나이지리아) 및 동남아시아 (인도)의 대표적인 국가들에 의해 설명할 수 있다.
 
 
 
아래의 식이 진짜 많은 것을 함축하고 있다.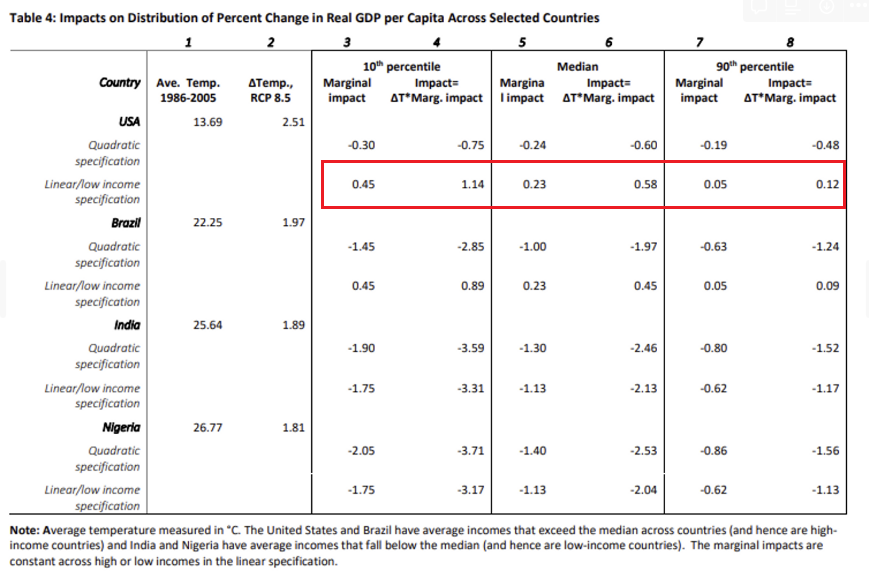

% change in real GDP → 가로 (1) Marginal impact는 linear specification 이고, (2) 두번째 요소는 quadratic specification 세로 (1) quadratic (2번째 식) (2) linear/low income specification (3번째 식) 을 보여준다. (표를 어떻게 정리하는지 잘 파악해 두어야 겠다)

미국은 비교적 온화한 (temperate)한 국기이다. 따라서 10th, median, 90th에서는 상대적으로 modest 한 모습을 보인다. 또한, 미국은 (Liner/low income specification에서) 고소득 국가이고, 이에 따른 추정된 계수는 양수 (+)가 나온다는 점이 신기하다. 이는 더 높은 온도가 경제 성장 분포를 상승시킨다는 것을 의미할 수 있다.
 
브라질은 따뜻하면서 고소득(high-income) 국가인데, 따라서 (Liner/low income specification에서) 조금 다른 결과를 보여주고 ‘온도’에 따른 차이를 잡아내 볼 수 있다. 고소득 국가가 경제적 영향을 적게 받고 실질 GDP 성장에 미치는 영향이 적을 수 있다고 정확하게 반영할 수 있다는 점을 시사한다. 또한 quandratic specification (두번째 열)은 차가운 나라의 온도 상승과 따뜻한 나라의 온도 상승과 관련된 차이를 살펴볼 수 있다. 더운 나라의 경우, 따뜻한 나라보다 작은 계수를 가지고 보인다.
 
인도와 나이지리아가 대표적으로 ‘높은 온도’이며 ‘저소득 국가’인데, 이는 기후 변화로 인한 성장 리스크에서, 이 논문이 하고 있는 “분위 회귀 접근 방식”의 핵심 결과를 보여줄 수 있다. 이 두 국가에서 온도 상승이 경제 성장의 하향 리스크를 크게 증가시키며, 실질 GDP 성장률의 하위 10%를 3%/2% p 낮춘다.
 
 

인도의 실질 GDP per capita 변화율 분포에 미치는 고온의 영향

두 가지 RCP 경로는 현재 정보와 예측을 고려할 때 하한과 상한을 나타낸다.

• 저배출(low-emission) 시나리오(Representative Concentration Pathway 2.6)에 따른 2040-59년 분포로, 이 경우1.1°C의 온도 상승을 가져올 수 있다.
• 고배출(high-emission) 시나리오(대표적 농도 경로 8.5)에 따른 2040-59년 분포로, 이 경우 1.9°C의 온도 상승을 가져올 수 있다.

 
(welfare) 이제는 welfare를 살펴본다. error term을 e(t)로 정의하고 특정 quantile q에 대한 quantile regression은 다음과 같은 손실 함수를 최소화할 수 있다.
$$ L=\sum_{t=1}^{T} q\langle e(t) I(e(t)>0)\rangle+(q-1)\langle e(t) I(e(t)<0)\rangle $$

• 낮은 quantile (q가 0.5 미만인 경우)에 대해서는 negative errors가 positive errors보다 큰 가중치
• median regression은 projection 으로부터 나오는 error의 최소 절대 편차를 최소화하는 계수

 
 
⇒ 특히 요즘은 기후 변화로 인해 경제의 위축(contractions)이 더 자주 발생하고 심각해질 수 있다. 이는 경제와 금융 안정성 (financial stability), 복지(welfare)에 중대한 영향을 또한 미칠 수 있다는 점을 다시 보여주기도 한다.