International asset pricing and exchange rate : Demand system approach

 

USDKRW 1327.69-1339.56 (2023.08.15)

오늘도 환율이 고공행진 중이다. 환율 시장이 떠들석 하고, 올해의 시장 화두는 "환율"인 만큼 관련 논문을 읽어보기로 했다. 최근 논문 동향은 이런식으로 정리 할 수 있고, 정리할 논문은 수요 측면에서 접근한 국제 자산 가격 결정 모형 관련한 논문이다. 

 

[선행 연구]

• 거시경제 변수와 금융 변수간의 연결 (comovements)
  • Rogoff (1996); Froot and Rogoff (1995); Frankel and Rose (1995)
• 국제 자본 흐름 (international capital flows) 이 환율 결정에 미치는 영향
  • Froot and Ramadorai (2005); Gabaix and Maggiori (2015)
• 시장 불완전성과 불균형에 의한 환율 결정
  • **화폐 공급 (currency supply)**이 완전히 탄력적이지 않으며, 화폐 수요 (currency demand) 충격이 환율에 영향을 미칠 수 있다는 이론적 근거에 관한 연구
  • Gabaix and Maggiori (2015) (QJE); Koijen and Yogo (2020); Greenwood et al. (2020); Gourinchas et al. (2020); Hau and Rey (2006) and Camanho et al. (2022)
• 헤지 및 리스크 관리에 기반한 환율의 움직임 분석
  • 국내 및 외국 투자자 간의 선물 환율 시장에서의 비대칭한 헤징 수요 변화가 선물 환율을 변경시키고 선물 환율과 현물 환율 시장 간의 화폐 환율 차익거래로 인해 환율 변동으로 이어짐
  • Carry trade 관련 연구
  • 포트폴리오 리밸런싱 (Portfolio rebalancing) 관련 연구
  • Evans and Lyons (2002, 2005, 2006); Rime et al. (2010); Menkhoff et al. (2016); Ranaldo and Somogyi (2021)) or FX swap rates (Cenedese et al. (2021); Syrstad and Viswanath-Natraj (2022); Czech (2021)
• 환율의 요인 분석 (dollar factor)
  • Lustig et al. (2011); Verdelhan (2018)

 

 

 

 

Exchange Rates and Asset Prices in a Global Demand System

저자 : Ralph S.J. Koijen and Motohiro Yogo (2019)

 

 

[주요 내용]

 

Koijen & Yogo는 국제 자산 가격 모형 (International asset pricing)을 통해 환율과 자산 가격의 변동 요인들을 분석한다. “수요 체계 분석”틀을 기반으로, 포트폴리오 선택과 시장 청산을 모형화하고 균형 가격을 도출한다.

• 대부분의 자산군 간 대체 (Substitution) 효과는 환율과 장기 수익률, 주식 가격과 연관이 있음을 확인할 수 있다.
• 또한, 중앙은행 정책이 환율 관리와 이자율 기간구조에 중요한 영향을 미친다는 것을 알 수 있다. 우선 1) 단기 금리는 환율 변동의 8%, 장기 수익률 변동의 9%를 설명하고 2) 장기채 보유량은 장기 수익률 변동의 9%를 설명한다. 3) 외환 보유고는 환율 변동의 19%, 장기 수익률 변동의 11%를 설명한다.
• US 자산의 수익률 (convenience yield)은 모든 자산군에서 크며, 특정 상태 (special-status)에 대한 중요성은 지리적으로 분산 (dispersed) 되어 있다는 점도 확인한다.

 

[데이터]

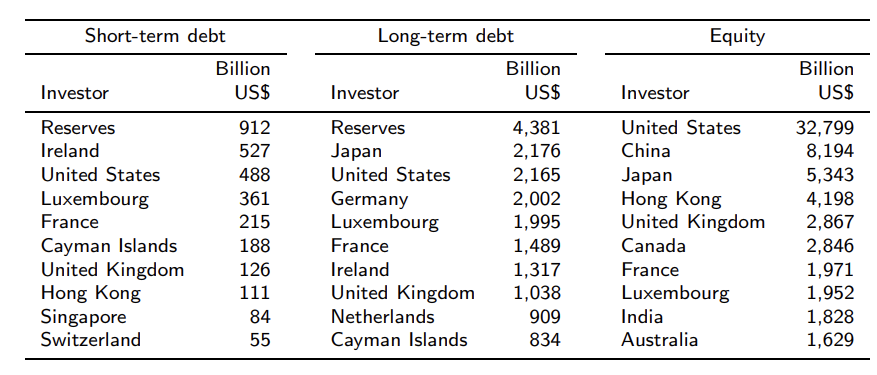
• 36개국의 환율 (Exchange rate), 자산 가격**, 거시 변수 (2002-2017) 데이터를 활용한다. IMF’s 의 조정된 포트폴리오 투자 survey를 기반으로 한 cross-country holdings
  • ** 자산군은 단기채 (short-term debt), 장기채 (long-term debt), 주식 (equity)을 활용
  • 투자자 (Investors) 88개국과 외환보유고 (reserve) 데이터를 활용
  • 공급 (supply) 측면에서는, 총 외국인 보유량 (debt)과 총 주식 (equity) 데이터를 활용

 

[모형 및 추정 방법론]

수요 시스템 접근 방식

• (1) 환율과 자산 가격들의 변동성을 분해 (decomposition), (2) 유럽 재정 위기와 같은 이벤트를 분석하고, (3) US 자산군의 Convenience yield (수익률)을 추정 (estimate)
• 국가 간 자산 보유량과 자산 가격을 매칭
  • 상대 수량 (quantities)과 가격 (prices)
  $$ \begin{array}{l}\text{Relative log quantity: } q_{t}(n)-q_{t}(\mathrm{US})\\\text{Relative log price: } p_{t}(n)+e_{t}(n)-p_{t}(\mathrm{US})\end{array} $$
  • 산점도를 그려보면, long-term debt와 equity에서는 비탄력적인 수요의 모습을 보임

 

(자산가격 모형)

Asset pricing (자산 가격 결정) = (1) 포트폴리오 선택 + (2) 시장 청산 (market clearing) 으로, 크게 두 가지 기본 틀로 전개를 한다. 투자자들의 포트폴리오 선택과, 이로 인한 자산 시장의 수요와 공급의 상호작용을 고려해서 결과적으로 자산 가격이 어떻게 결정되는지 보여준다. 하나하나 뜯어서 분석해 볼 수 있다.

 

(1) 시장 청산 (Market Clearing)

 

먼저, 시장 청산이란 경제에서 수요와 공급이 균형을 이루는 상황을 말하며, 자산 가격 형성에 중요하다. 특히 자산 가격은 다양한 변수와 요인들이 상호 작용해서 가격이 조정되고 균형 가격이 결정 된다.

해당 모형에서는 각 국가 n 과 자산군 l 이 있을 때, 좌변 (LHS)은 공급 (가격 x 수량), 우변 (RHS)은 수요 (투자자의 wealth x 포트폴리오 비중) 를 나타내는 방정식을 그려볼 수 있다.

 

$$ \underbrace{ P_{t}(n, l) E_{t}(n) Q_{t}(n, l)}_{수요}=\ \underbrace{ \sum{i=1}^{l} A_{i, t} w_{i, t}\left(n, l ; \mathbf{P}{t}, \mathbf{E}{t}\right)}_{공급} $$

• $P_{t}(n, l)$ : Market-to-book 비율 (액면가 한 단위 당 가격)
• $E_{t}(n)$ : 타국가 (n) 통화 한 단위 당 미국 달러 )Exchange rate in US$ per country n’s currency unit)
• $Q_{t}(n, l)$ : 타국가 (n)의 통화 한 단위 (currency)로 환산한 장부 가치 (Book value)
• $w_{i, t}(n, l)$ : 국가 n 및 자산군 l 에 대한 포트폴리오 비중
  • 국가 간 보유량를 일치시킴 (match cross-country holdings)
  • 수요 탄력성은 추정이 용이하며, 자산군 내 및 자산군 간 대체 가능
• $A_{i,t}$ : 투자자 i 의 wealth

 

(2) 포트폴리오 선택 (Portfolio Choice)

 

평균-분산 (Mean-Variance) 포트폴리오는 각 투자자가 자신의 선호와 기대 수익률을 고려해서 자산을 선택하고 분배하는 방식을 모형화한다. 다음과 같으며, 수익에 대해서 (투자자마다) 이질적인 (heterogeneous) 믿음 (belief)를 가진다.

$$ \mathbf{w}{i}=\Sigma{i}^{-1} \mu_{i} $$

 

이때 두 가지 가정이 사용된다.

1. 공분산 행렬은 요인 구조 (factor structure)를 가진다.
2. 기대 수익과 팩터 로딩 (factor loading)은 관찰된 특성 (characteristic) 에 기반한다.

 

(추정 방법론) 이때, 중요한 것은 “**포트폴리오 비중”**이다. 그러나 앞서 비중은 **기대 수익 ($\mu_i$)**에 의존하게 되므로 먼저 $\mu_i$ 에 대해서 추정을 해야 한다. 다음은 각 자산군(l)에 대한 예측 회귀분석 결과를 나타내는 식이며, 자산군(n)의 초과 수익률($r_{t+1}(n, l)$)과 미국의 수익률($y_{t}(\mathrm{US})$) 사이의 관계를 설명한다.

 

$$ r_{t+1}(n, l)-y_{t}(\mathrm{US})=\theta_{l} p_{t}(n, I)+\Theta_{l}\left(e_{t}(n)-z_{t}(n)\right)+\nu_{t+1}(n, I) $$

• $\Theta_{l}$: 국가 n의 자산 군 l의 환율에 대한 회귀 계수
• $\theta_{l}$: 국가 n의 자산 군 l의 수익률에 대한 회귀 계수

 

기대 수익률(Expected returns) in investor i’s currency unit

$$ \mathbb{E}_{t}\left[r_{t+1}(n, l)-\Delta e_{t+1}(i)-y_{t}(i)\right]=\mu_{i, t}(n, l) $$

 

포트폴리오 선택은 자산 수익률, 특성 정보, 투자자의 개별적인 선호도 등을 고려해서 이루어 진다. 다음으로, 포트폴리오의 비중을 로짓 (logit) 모형 기본 구조로 표현하면 다음과 같다.

 

$$ \log \left(\frac{w_{i}(n)}{w_{i}(0)}\right)=\beta p_{i}(n)+\gamma^{\prime} \mathbf{x}_{i}(n)+\epsilon_{i}(n) $$

• $w_{i}(n)$: 국가 n에서의 투자자 i의 포트폴리오 가중치
• $w_{i}(0)$: 특정 기준 국가 (미국)에서의 투자자 i의 포트폴리오 가중치
• $p_{i}(n)$ : 국가 n에서의 자산 수익률
• $\mathbf{x}_{i, t}(n, l)$ : 관찰된 특성** (characteristic) (거시 변수 및 Bilateral 정보)
• $\epsilon_{i, t}(n, l)$ : 잔차 (잠재 수요 (lantent demand)를 나타냄)

 

** 이때, 관찰된 특성으로는 거시 변수는 log GDP, log GDP / capita, inflation, equatiy volatility, sovereign debt rating이 있으며, Bilateral (양국 관계) 정보로는 수출/수입(Export/Import) 비중과 거리 (distance). 더미 변수는 각 국가의 자국 편향 (home bias), 특정한 사건? (specialness) 관련된 년도 등을 포함시켜 관찰되는 정보들은 발라내준다.

 

 

• 나아가, 자산군 내 불완전한 대체 가능성 (imperfect substitution across asset classes)을 다루기 위해선 다음을 고려해 볼 수 있다.

$$ w_{i, t}(n, I)=\underbrace{w_{i, t}(n \mid I)}_{\text {within }} \underbrace{w{i, t}(I)}_{\text {across }} $$

 

(표 해석) 위 표는 36개 국가의 단기채, 장기채 및 주식에 대한 패널 회귀분석의 결과 보고식인데, 로그 MoB비율과 실제 환율은 모든 자산군에 대한 초과 수익률의 유의미한 예측 요인으로 나타난다. 단기채의 경우, 실질 환율의 추정 계수가 -0.31으로 환율이 1% 증가할 때마다 88 bp 증가한다는 것을 나타낸다.

 

• 또한 포트폴리오 비중은 자산군 내(within asset) 에서는,

$$ w_{i, t}(n \mid l)=\frac{\delta_{i, t}(n, l)}{1+\sum_{m=0}^{N} \delta_{i, t}(m, l)} \\ \\ where \ \log \left(\delta_{i, t}(n, l)\right)=\beta_{I} \mu_{i, t}(n, l)+\gamma_{l}^{\prime} \mathbf{x}{i, t}(n, l)+\epsilon{i, t}(n, l) $$

Substitution within asset class

$$ \Rightarrow \log \left(\frac{w_{i, t}(n \mid l)}{w_{i, t}(0 \mid l)}\right)=\beta_{l} \mu_{i, t}(n, I)+\gamma_{I}^{\prime} \mathbf{x}{i, t}(n, I)+\epsilon{i, t}(n, I) $$

 

(표 해석) 자산군 내 수요에 대해서 추정된 계수를 나타내는데, 단기채의 경우 기대수익률에 대한 계수가 31.53이며 수요 탄력성 (demand elasticity)은 42이다. 이는 가격이 1% 상승할 때 단기채 수요가 42% 감소함을 의미한다. 또한 거시 변수에 대한 계수 부호 (sign)이 자산군 간에 유사함을 알 수 있다. GDP와 GDP/Capita 는 양수인데, 이는 발행국의 사이즈와 wealth 가 클수록 수요가 증가한다는 것을 의마한다. 인플레이션이 1%p 증가할 때, 장기채 수요는 22% 감소한다.

 

 

• 자산군 간 (across asset)에서는 다음과 같이 표현을 정리해볼 수 있다.

 

$$ w_{i, t}(I)=\frac{\left(1+\sum_{m=0}^{N} \delta_{i, t}(m, I)\right)^{\lambda_{l}} \exp \left\{\alpha_{I}+\xi_{i, t}(I)\right\}}{\sum_{k=1}^{3}\left(1+\sum_{m=0}^{N} \delta_{i, t}(m, k)\right)^{\lambda_{k}} \exp \left\{\alpha_{k}+\xi_{i, t}(k)\right\}} $$

Substitution across asset classes

 

$$ \Rightarrow \log \left(\frac{w_{i, t}(I)}{w_{i, t}(3)}\right)=-\lambda_{l} \log \left(w_{i, t}(0 \mid I)\right)+\lambda_{3} \log \left(w_{i, t}(0 \mid 3)\right)+\alpha_{l}+\xi_{i, t}(I) \\ =-\lambda_{l} \log \left(w_{i, t}(0 \mid l)\right)+\lambda_{3} \log \left(w_{i, t}(0 \mid 3)\right)+\alpha_{l}+\xi_{i, t}(l) $$

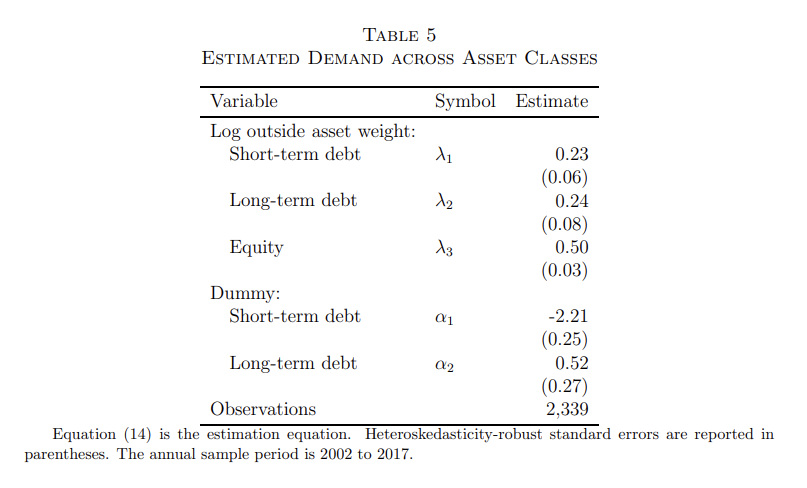
(표 해석) 자산군 간 수요에 대한 추정 계수를 나타내는데, 각 자산군에 대해서 외국 자산 가중치에 대한 계수가 주어진다. 이 계수는 유의마하며, 자산군 간 대체 가능성이 환율과 자산 가격에 중요한 역할을 함을 시사한다.

 

 

 

[분석 및 주요 결론]

 

(Variance Decomposition) Market clearing 을 통해, 환율과 자산 가격들을 내재 함수 (implicit function) (g(.))로 정의한다.

$$ \left[\begin{array}{c}\mathbf{e}{t} \\\mathbf{p}{t}(2) \\\mathbf{p}{t}(3)\end{array}\right]=g\left(\mathbf{x}{t}, \mathbf{z}{t}, \mathbf{p}{t}(1), \mathbf{Q}{t}, \epsilon{t}, \xi_{t}\right) $$

 

 

** 이때, 통화정책 충격 같은 변수는 직접 결정되지 않는 변수로 단기채 수량 등에 의해서 결정 된다고 가정. 잠재 수요는 중앙은행 정책에 의해 결정되는 외환 보유액의 잠재 수요 및 투자자 국가에 대한 것으로 분리좌변은 환율, 장기 채권 가격, Market to book 벡터를 의미하고, 우변은 자산군 특성, 상대 CPI, 상대국 자산 (outside assets), 단기 채권 가격, 자산 보유량 (asset quantities), 잠재 수요 (latent demand), 자산군 잠재 수요 (asset-class latent demand)를 의미한다.

 

(그림 해석) 단기채 시장 규모로 가중된 환율의 분산 분해 (Variance decomposition)를 나타내는 표이다. 환율 변동은 거시 변수 (26%), 외환보유고 (19%), 단기금리 (8%), 부채 (2%) 등 근본 요인들이 55%를 구성한다. 나머지 45%는 잠재 수요로 설명이 된다. North American investors substituting across asset classes 이 8%, 유럽도 마찬가지로 8%로 설명된다.