Subjective Bond Returns and Belief Aggregation (The Review of Financial Studies)

Subjective Bond Returns and Belief Aggregation (2022)
저자 : Andrea Buraschi, Ilaria Piatti, Paul Whelan
The Review of Financial Studies

 
데이터를 예측하거나 추정하는 방법은 정말 여러가지가 있다. 하나의 좋은 방법을 찾는 것이 쉽지 않기 때문에 여러 방법론을 조합해서 결과치를 내고, 이를 평균 내어 결과 값을 최종 도출해서 정확도를 높이는 방식으로 이용하는 방법이 최근에 제시되고 있다. 특히 예상 수익률 추정은 경험적인 자산 가격 결정의 중요한 원칙이다.

 

사실 이 방법론에 대해서는 약간 회의적이기도 하다. 서로 다른 방법론에 의해 도출된 값에 평균을 취한다는 것이 납득이 잘 되지 않는다. 평균의 맹점은 생각보다 다양하게 나타나기 때문이다. 이 논문은 그런 맹점! 을 극복하기 위해 평균을 취하는 것은 적용하되, 각 결과치마다 다른 가중치를 적용하는 척도 (measure)를 제시한다. 기존의 예측값이 더 실제 값과 가까웠다면 더 큰 가중치를 주는 방법론을 활용을 한다.

 

구체적으로, 이 논문은 이질적인 (Heterogenous) 기대치들의 종합 (aggregation)이 예측의 정확성을 향상시킨다는 것을 채권 수익률을 통해 보여준다. 전문적인 이자율 예측 기관들의 과거 정확성을 기반으로 수익률 기대치의 종합 방법을 제안한다. 간단하게 말하자면, 기존에 잘 예측했던 기관에 더 큰 가중치를 주어서 종합하는 새로운 방법론을 제시하는 것이다. 동등 가중치와 중간 가중치 조합을 능가하며, 그 동적 특성은 매우 다르지만 통계적 예측과 유사한 결과를 보여준다.

 

조금 더 구체적으로 정리하면, 기대치의 cross section에서 유용한 정보를 무시할 수도 있다는 생각 (idea)에 영감을 받아 주관적인 채권 수익률 예측의 종합 (Aggregation) 치를 연구하며, 월별 패널 데이터를 사용하여 미래 미국 국채 수익률에 대한 전문적인 시장 참가자들의 기대치를 추정한다.

 

먼저 주관적인 채권 수익률 중에 좋은 예측치를 내는 것을 선별하기 위해서는 먼저, 1) 정확도의 지속성을 판단해야 한다. 한 시기에 잘 예측을 했지만, 다음 시기에 잘 예측을 잘 하지 못한다면 해당 방법론이 무용지물이 되는 것이다. 2) 실시간 가중치를 개별 기대치에 적용한다. 즉, 역사적으로 좋지 않은 전문기관의 예측치를 제외하고, 남은 예측을 잘하는 집단의 기대치로 종합 (Aggregation)을 구성하는 것이다. 이 때의 measure 방법을 분위수와 랭킹 (순위) 방법을 이용한다는 점이 특징이다.

 

1), 2) 가 이 방법론을 어떻게 정당화 시키고, 어떤 measure를 이용하는지, 추정 방법은 어떤 것인지 잘 파악해야 한다. 그리고 결국 설명하고자 하는 바는, 이 척도를 이용해서 “위험의 양 (quantities of risk)”과 “위험에 대한 보상 (compensation for risk)” 관계를 보여주는 것이며, 실현된 수익률을 통해 이 관계가 감지하기는 어려운 주관적 기대 (subjective expectation)과 강한 연관성이 있다는 것을 증명한다.

 

 

[데이터]

• BlueChip Financial Forecasts (BCFF) **에서 제공하는 Subjective expected excess bond returns 의 1998.01~2020.01 월별 서베이 데이터를 사용한다.
  • ** BCFF는 U.S.의 모든 만기의 수익률 곡선, GDP와 인플레이션 등 주요 거시 데이터에 대한 금융 기관 (financial institution) 의 기대치를 panel data로 제공

 

[measure 1] Subjective excess bond returns

주어진 미래 이자율에 대한 기대가 주어진다면 (아래 식에서 Survey yield forecasts 부분), 개인의 subjective expected excess bond return을 measure 할 수 있고 다음과 같은 식을 활용한다.

$$ e r x_{i, t}^{n}=-(n-1) \times \underbrace{E_{t}^{i}\left[y_{t+12}^{n-1}\right]}_{\begin{array}{c}\text { Survey Yield } \\\text { Forecasts }\end{array}}+n y{t}^{n}-y_{t}^{1} $$

• $p_{t}^{n}$ 은 무위험 제로쿠폰의 t시점 가격이다. 이때 이 제로 쿠폰은 미래 n 년의 한 단위 지불 가격이라고 보면 된다.
• $y_{t}^{n}=-\frac{p_{t}^{n}}{n}$ 는 연속 복리 spot 수익률 (Continuously compounded spot yields)
• 위의 주어진 식을 통해, 1년 예측 기간 동안의 EBRs (expected excess bond returns)의 implied 된 값, 즉 내재된 값을 도출할 수 있다.

 

 

주관적인 채권 수익률이 (1) 큰 이질성이 있을 때 유의미하게 뛰어난 예측가들이 있을 수 있음을 알 수 있다. 다만 이것만으로는 부족하다. (2) 예측 정확도의 “지속성”이 있어야 이 논문의 목표인 “가중” 평균을 제시할 수 있는 것이다.

 

[measure 2] 

(1) 정확도의 이질성 (Heterogeneity in accuracy)

예측 능력에 대한 이질성 (heterogeneity)에 대한 평가를 위해서 예측 오차를 이용한다. 각 agent 는 i로 표현하고, 총 $T_i$ 가 존재한다.

$$ \begin{aligned}F E_{i, t+12}^{n} & =r x_{t+12}^{n}-e r x_{i, t}^{n} \\M S E_{i}^{n} & =\frac{1}{T_{i}} \sum_{t=1}^{T_{i}}\left(F E_{i, t+12}^{n}\right)^{2}\end{aligned} $$

• $M S E_{i}^{n}$ : Mean squred errors (one year horizon)
• $F E_{i, t+12}^{n}$ : forecast errors
• $r x_{t+12}^{n}$ : realized excess return on an n-period bond

이 논문에서는 MSE 외에도 SME와 EVAR를 같이 활용한다.

 

(그림 해석) unconditional heterogeneity는 정확성에서 채권 만기와 10-year 채권 모두에서 MSE분포가 양의 왜도를 가짐을 보여준다. 오른쪽은 Diebold and Mariano (1995) (DM) 통계량을 활용한다.

 

 

(2) 정확성의 지속도 (Persistence in accuracy)

MSE에 대한 연간 전환 확률을 계산한다. MSE의 분포에서 특정 분위수에 있는 예측가들이 다음 해에 동일한 분위수에서 머무를지 측정한다.

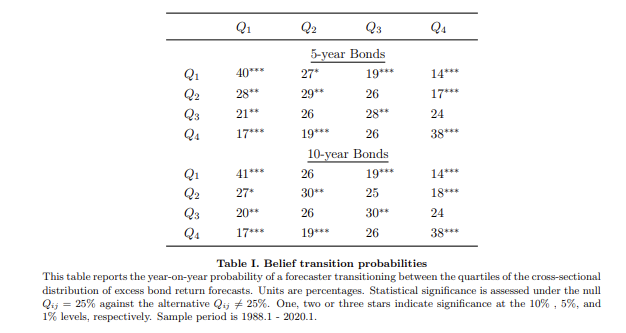
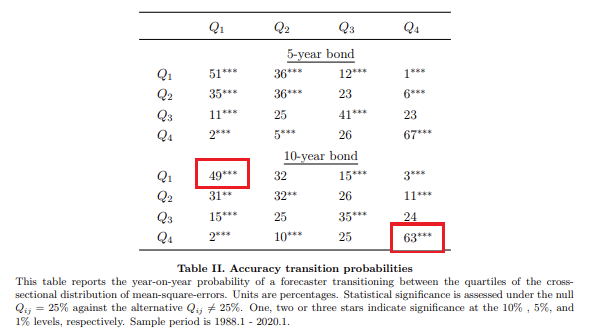
(그림 해석) 10년 만기 채권의 경우, 좋은 예측가 (Q1)** 가 다음 해에 좋은 예측가가 될 확률이 49%이다. 나쁜 예측가 (Q4) 는 다음 해에 그대로 남아있을 확률이 63%이다. 흥미로운 점은 “정확성의 지속도”가 “믿음의 지속성”보다 더 강하다는 점도 알 수 있다.

** 좋은 예측가는 더 근접하게 수익률을 예측한 기관을 말하며, 1분위수에 속하는 곳이라고 생각하면 됨

 

 

[aggregation method]

이렇게 좋은 예측가들이, 지속적으로 예측을 할 수 있다고 결론을 내린다 하더라도, 실제로 ‘좋은 예측가’들을 사전에 식별 가능하다는 것을 의미하지는 않는다. 이 때문에 실증적으로는 간단한 평균이 이론적으로 최적인 가중치 구현보다 종종 더 우수한 성능을 보이는 이른바, “동일 가중치의 퍼즐 (the equal weights puzzle)”이 나오는 것이다.

이 논문의 방법의 특징은 모델을 추정하는 방법을 활용하지 않는다* 는 것이다. 정확도** 가 높은 예측가에게 더 많은 가중치를 부여하며, 시간이 지남에 따라서 예측 환경이 자유롭게 달라질 수 있음도 전제하고 있다.

• 이 방법은 unbalanced panels 에도 용이하게 이용 가능

** 특히, 예측 오차 수준 대신 historical 랭킹을 활용한다는 점을 주목

 

 

[방법론]

(Forecast aggregation)

“동일 가중”으로 추정한 주관 채권 수익률을 $E B R^{c}$ 이라 한다면, $E B R_{t}^{\star, n}(N, Q)$ 은 “조건부” 주관적 채권 수익률을 나타낸다. $\mathcal{R}_{i t}$ 는 평균 분위수 ranking을 measure 한 지표이다. 여기서 중요한 것은 Q인데, 잔인하게도 어떤 예측가를 버리고 어떤 예측가를 보존할지 결정한다.

• step1. [t-N, t]에서 예측 오차의 값을 계산하고, 백분율 순위 패널로 변환
• step2. 각 시간 t에 예측가에 대해서 rolling window [t-N, t]의 중앙 (median) 백분위 순위를 계산
• step3. 중앙 백분위 순위에서 상위 Qth 백분위를 가지는 agent 들을 꼽고 나머지는 가중치 0을 부여
• step4. 선택된 예측가의 기대치를 과거 역사적 순위의 정확성에 따라 선형 가중치로 조합

(그림 해석) (a)에서 동역학을 눈으로 살펴보면 주관적 예상 초과 채권 수익률이 역주기적인 경향을 보인다. 또한 두 그림은 측정치 간 스프레드가 매우 큰 경우를 보여준다. 1999년 말 인터넷 버블이 붕괴되기 직전에 19년 만기 채권 스프레드가 200 bp를 초과했다는 점을 고려해 볼 수 있다. 또한 큰 음의 스프레드는 잘 나타나지 않는다는 점도 확인할 수 있다.