The Market Price of Risk and Macro-Financial Dynamics

The Market Price of Risk and Macro-Financial Dynamics (2023)
저자 : Tobias Adrian, Fernando Duarte, Tara Iyer
Centre for Economic Policy Research Discussion Paper

 

Financial-Macro dynamic 에 관해 연구하면서 제일 많이 이름을 접한 Adrian 님의 working paper가 나왔다.  

 

Financial 과 Macro의 영향 관계에 대해서는 실제 경제 현상에서 우리가 마주하게 될 크고 작은 문제들과 밀접하게 연결이 되어 있다. 다만, 이 복잡한 현상에서 동학적인 메커니즘을 찾아서 분석하기는 쉽지 않다. 아니 불가능 하다.

 

그래서 실증 분석에서는, 금융 조건을 대표하는 지표를 뽑아서, 이게 거시 경제에 미치는 영향을 확인한다. 다만, 이 금용 조건을 대표하는 지표가 실제로 진짜 우리가 마주하는 금융 상황 위기를 “대표”할 수 있냐는 것에 대해서는 잘 설명할 수 있어야 한다. 그리고 이거를 잘 설명해서 보여주려고 하는 노력이 이어지고 있는 것이다.

 

이런 맥락에서, <The Market Price of Risk and Macro-Financial Dynamics> 논문에서는 가격 변수와의 상호 작용에 대한 실제 Macro-finance 이론의 기초를 마련하고 있으며, 이런 동학적인 분석을 고려했을 때, VFCI 가 다른 FCI 지표들 보다 더 나은 설명을 할 수 있는지 보여주고 있다.

 

위 논문은 크게 두 축으로 정리할 수 있다. 1) VFCI 지표를 측정 (measure) 하는 것과, 이 지표를 기반으로 2) Macro-Financial dynamic 을 설명하는 것이 그것이다. 다른 말로 해보자면, 펀더멘털로부터 비롯되는 FCI (Financial Condition Index)를 사용해서 1) 위험의 가격화 (pricing of risk) 와 2) 통화정책 (Monetary policy) 사이의 동학적인 (dynamic) 피드백 효과가 있음을 확인한다.

 

이에 따른 주요 결론은 모형을 통해 도출한 VFCI 지수는 다른 FCI와 비교해서 주식 및 채권 프리미엄을 더 잘 설명한다. 또한, 금융 조건이 긴장 (tightening)되면 즉시 통화정책이 완화되고, 지속적으로 경제가 위축된다. 반면 긴축 통화정책 충격은 금융 조건을 악화시킨다는 것을 확인한다.

 

[주요 내용]

• 이론에 기반하여 새로운 FCI 지수를 도출하고, 이를 “리스크의 시장가격”이라고 보았다. VFCI는 금융 자산 수익률에 의해서 Spanned 되는 GDP 변동성 (volatility)를 추정한다.
• 이 지표를 기반으로 Macro-financial dynamic에 대해서 분석한다. 이때, 다양한 식별 방법론과 도구변수들을 사용한다.
  • 가장 기본 모델은 Conditional heteroskedastic BVAR로 분석하고, SVAR, local projection, 부호 제약 방법론을 사용해서 이 지표가 해당 현상을 잘 설명하는지 식별하기도 한다. 또한 VFCI와 통화정책, GDP를 도구변수로 활용한다.
• 이때 VCFI tightening 충격은 통화정책을 즉시 즉각적으로 완화시키고, output 의 지속적인 수축 (contraction)을 만들지만, 인플레이션에 영향을 주지는 않는다는 결론을 도출해낸다.

 

[VFCI 모형 및 추정]

• 관측 가능한 금융 변수는 $F_t$ 이며, $X_t$ 는 금융 요인 (factors)의 벡터이고, 금융 상태 요인의 affine 함수 (function)이다. $F_t$로부터 $X_t$ 요인을 추출해 내고 이때 PCA (주성분 분석; principal components analysis) 필터링 기법을 사용한다.
• [conditional heteroskedastic linear regression]
  • **변동성 (variance)**은 평균 방정식에서 regressors의 지수 함수이다.
  • (추정) ML (Maximum Likelihood) 방식을 활용한다.
  • The VFCI is the (log of the) predicted conditional volatility of GDP

$$ \begin{aligned}\Delta g d p_{t} & =\theta P C_{t}+\varepsilon_{t} \\\sigma_{t}^{2} & =\exp \left(\delta P C_{t}\right)\end{aligned} $$

$$ V F C I=\log \sqrt{\hat{\sigma}{t}^{2}}=\hat{\delta} P C{t} $$

 

 

[이론적 토대]

• No arbitrage (무차익조건) 는 모든 자산을 가격화하는 SDF의 존재성을 함의하고 있다고 볼 수 있다.
  • 이는 다음과 같이 분해 (Decompose)할 수 있다.
    • $\varepsilon_{t+1}$ 는 fundamental 충격 벡터이고, $\lambda_{t}$ 은 리스크 가격이다.

$$ \begin{aligned}S D F_{t+1} & =\mathbb{E}_{t}\left[S D F_{t+1}\right]+\left(S D F_{t+1}-\mathbb{E}{t}\left[S D F{t+1}\right]\right) \\& =\mathbb{E}_{t}\left[S D F_{t+1}\right]+\lambda_{t} \varepsilon_{t+1}\end{aligned} $$

$$ 1=\mathbb{E}_{t}\left[S D F_{t+1} R_{t+1}\right] $$

• 이때, utility는 CRRA 형태를 가정하면 다음과 같이 정리할 수 있다.$$ \Rightarrow \begin{aligned}\Delta c_{t+1} & =a+b S D F_{t+1} \\& =a+b \mathbb{E}_{t}\left[S D F_{t+1}\right]+b \lambda_{t} \varepsilon_{t+1}\end{aligned} $$

$$ \begin{aligned}S D F_{t+1} & =\exp \left(\log \beta-\gamma \Delta c_{t+1}\right) \\& \approx 1+\log \beta-\gamma \Delta c_{t+1}\end{aligned} $$

• Representative Agent의 F.O.C를 기반으로 소비 (consumption)와 SDF를 연결시킬 수 있다.이때 $\operatorname{Var}{t}\left(\epsilon{t+1}\right)=\operatorname{Var}\left(\epsilon_{t+1}\right)=1$ 이며, $\sigma_{t} \equiv b \sqrt{\operatorname{Var}{t}\left(\lambda{t} \varepsilon_{t+1}\right)} =b\left\|\lambda_{t}\right\|$ 이라고 설정할 수 있다.

$$ \begin{aligned} \Delta c_{t+1} & =a \pm b \mathbb{E}_{t}\left[S D F_{t+1}\right]+b \lambda_{t} \varepsilon_{t+1} \\ & =a+b \mathbb{E}_{t}\left[S D F_{t+1}\right]+\sigma_{t} \epsilon_{t+1} \end{aligned} $$

• 이제는 리스크 가격 (VFCI)를 다음과 같이 정의할 수 있다.

$$ V F C I_{t} \equiv \log \sigma_{t}^{2} $$

 

 

[데이터]

이때 사용하는 금융 데이터는 다음과 같다.

 

$$ \begin{array}{ll}\hline \text { Variable } & \text { Description } \\\hline \hline \text { SP500RET } & \text { Equity market returns - S\&P500 annual returns } \\\text { SP500SD } & \text { Equity market volatility - S\&P500 annualized daily standard deviation } \\\text { T10Y3M } & \text { Term spread of } 10 \text { year over } 3 \text { month Treasuries } \\\text { 3MY-FF } & \text { Spread of } 3 \text { month Treasuries over Federal Funds rate } \\\text { AAA-10Y } & \text { Spread of Moody's AAA corporate bond yield over 10 year Treasuries } \\\text { BAA-AAA } & \text { Spread of Moody's BBB corporate bond yield over AAA bond yield } \\\hline\end{array} $$

 

이때, VCFI 는 4개의 주요 주성분으로 추정된다. (88% of variance)

 

 

기존에 자주 사용되는 FCI 와 비교

NFCI	GSFCI	VIX
Chicago Fed’s National Financial Conditions Index	Goldman Sachs Financial Conditions Index	Market’s expectation of future volatility based on options of the S&P 500

통계적으로 다른 FCI 지수보다 VFCI가 위험 프리미엄 (risk premia)를 잘 설명한다.

 

 

[Macro-Finance dynamics 분석]

취약성 (Financial tightening)이 통화정책 완화와 생산 수축 (contraction)로 이어진다. 반대로 , 긴축 통화 정책과 생산 역성장이 금융 조건의 악화를 가지고 온다.

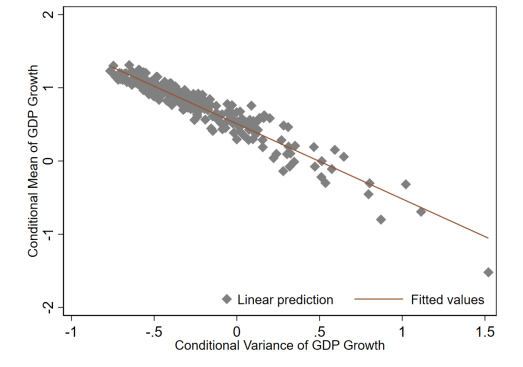
• 이때 금융 취약성을 measure 하는 지표가 VFCI 이다. VFCI 는 GDP 성장의 조건부 평균에 밀접하게 연관이 되어 있기 때문에 이를 활용해 볼 수 있다. FCI가 낮은 예상 성장률을 가진 기간은 높은 변동성을 가지기 때문에, Growth at risk 분포에서 음의 왜도를 생성한다. 즉, 금융 조건이 더 클수록, 하방 리스크가 증가하게 되며 취약한 성장 (Vulnerable gorwht)로 이어질 수 있음을 설명한다.

$$ \text X_{t}=\left[\log G D P_{t}, \log P C E_{t}, \text { FedFunds } t, V F C I_{t}\right] $$

 

 

[Heteroskedasticity 모형]

기본적인 volatility-identified VAR 모형은 다음과 같으며 Bayesian 방법론을 사용한다.

 

$$ A_{0} y_{t}=\sum_{j=1}^{p} A_{j} y_{t-j}+\varepsilon_{t} $$

 

이때, 오차항 $\varepsilon_{t}$가 $(0, \sigma_{\varepsilon})$ 분포를 따르지만, volatility-identified VAR 모델에서는 $\varepsilon_{t}$의 조건부 분산이 시간에 따라 변동할 수 있다는 점을 특징으로 꼽을 수 있다. 이는 특정 변동성 변화점 $m \in M$ 에서 변동성이 변화하는 것이라고도 할 수 있으며, 변동성이 변화는 상황을 더 정확히 모델링 할 수 있다.

$$ E\left[\varepsilon_{t} \varepsilon_{t}^{\prime}\right]=\Lambda_{m, t} $$

 

Volatility regimes in the BVAR

 

 

(추정)

student-t (asymmetry 한 분포를 가짐) 분포를 가진 베이지안 VAR를 추정한다.

이때, 20Q 에 걸쳐 10,000개의 MCMC 추출을 시뮬레이션 하여 얻은 Median IRF 를 보고 (reporting)한다.

** IRF는 추정해서 얻은 결과값을 reporting 하기 위한 방법이다.

 

(표 해석) 결과를 보면, 다양한 국면 (regimes)에서, 충격의 Posterior relative variance (사후 분산) 이 상당히 다를 수 있음을 확인할 수 있다. 즉, heterogeneity한 모습을 잘 확인할 수 있다.

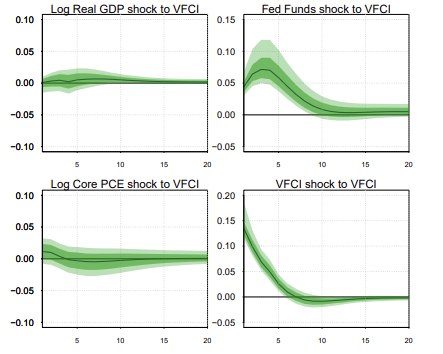
(그림 해석) VFCI 에 1 \sigma 충격을 주었을 때, 거시 변수의 반응을 보여준다. 실질 GDP 는 6분기에 걸쳐서 0.4”%” 감소했고, Federal fund rate는 7분기를 정점으로 0.2% 완화 (easing) 된다. Core PCE의 영향에 대한 영향은 weak한 evidence를 보인다.

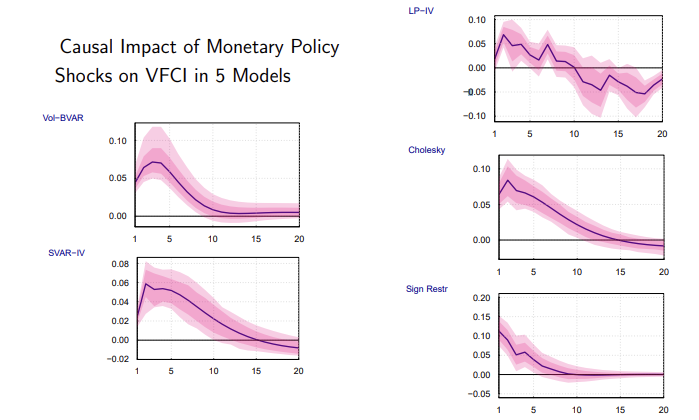
(그림 해석) 이제 반대의 경우이다. 경제 변수의 1 \sigma 충격이 금융 조건 (Financial condition)에 미치는 영향을 IRF 로 그려본다. 오른쪽 가장 위의 그래프에 집중해 보자. 통화정책 충격이 왔을 때, VFCI 는 5% tightening (긴장)되고, 3분기에 약 7.5% 까지 증가하여 3년간 서서히 감소한다.

 

자, 이제 위험의 가격 (VFCI)의 dynamic한 영향과 반응이 robustness 한지 의심해 볼 수 있다. 그래서 식별 (identification techniques)이나 다양한 도구 변수 (instruments)로 강건성 (robusteness) 을 설명해 볼 수 있다.

 

[Instruments 도구변수]

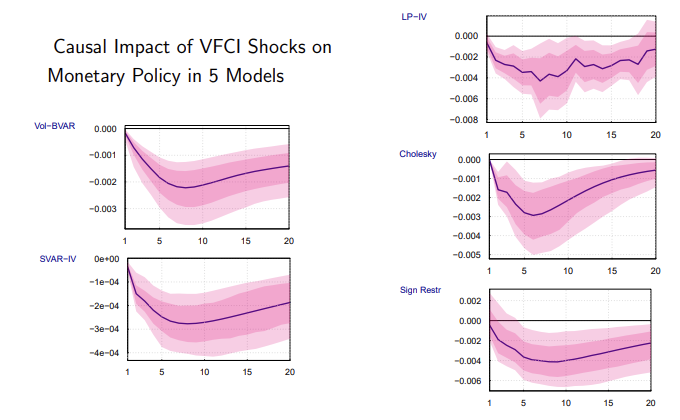
(분석 결과) 여러 도구변수를 이용해서 식별한 결과를 보여주는데, 대부분 모형에서 일관성을 가지는 모습을 볼 수 있다.

• 통화정책 (monetary policy) 도구변수 (Nakamura and steinsson 2018) : high-frequency 을 통해 식별
• GDP 성장 도구변수 (Cieslak and Pang; 2021) : 채권과 주식의 뉴스에 따른 반응을 부호 제약으로 식별
• VFCI 도구변수 금융 조건이 긴장 (tightening) 충격의 영향이 가격을 감소시킨다는 것을 이용해 부호를 제약