Macro Risks and the Term Structure of Interest Rates

Macro Risks and the Term Structure of Interest Rates (AER) 

저자 : Bekaert, Engstrom, Fordham

 

위 논문에서는 BEGE (Bad Enviornent - Good Enviornment) 해석을 활용하는데, 이때, B(ekaert), E(ngstrom), G(Eert), E(ric) 는 본인들 이름을 의미하기도 한다고. 앞의 decomposition supply/demand driven inflation 자료와도 연결할 수 있다. 이 자료는 수요/공급 충격을 inflation과 연결했다면 여기서는 risk와 연결을 시켰다고 생각하면 된다.

 

[주요 내용]

• 채권 위험 프리미엄에 상당한 변동성이 있는데, “거시 위험” 대신에 “**거시 수준 (level) 요인”**을 활용하는 것이 채권 수익률 예측에 도움이 된다고 말한다. 구체적으로, 거시 위험 변수를 포함한 매크로 수준 변수들이 수익률 변동의 80%를 설명한다. 또한 내재된 위험 프리미엄은 counter-cyclical 함. 인플레이션 위험 프리미엄을 통해서, ****70년대 높은 스태그플레이션, 대공황 시기의 낮은 인플레이션의 원천?에 대해서도 설명한다.
• 위의 프리미엄 변동에 대한 설명을 AS/AD 해석과 연결시킨다는 점이 이 논문의 주요 특징이다. 직관적으로, 총공급 AS (Aggregate supply) 환경에서 인플레이션과 채권 위험 프리미엄은 높아질 것이고, 총수요 AD (Aggregate demand) 환경에서는 위험과 만기 프리미엄이 감소한는 것을 설명한다. 본 논문은 이런 AS/AD의 관점에서 본 거시 위험과 기간 구조를 연결시켜 설명을 한다.
  • 자산 가격을 결정할 때, 비가우시안 분포 를 사용

 

[주요 내용]

(AS/AD 와 거시 모델링) 먼저 AS/AD 환경에서 거시 변수 (실질 성장과 인플레이션)가 어떤 방향으로 나타나는지 우선 모델링한다.

실질 성장과 인플레이션 충격을 다음과 같이 나타낸다.

$$ \begin{aligned}g_{t} & =E_{t-1}\left[g_{t}\right]+u_{t}^{g}, \\\pi_{t} & =E_{t-1}\left[\pi_{t}\right]+u_{t}^{\pi}\end{aligned} $$

위의 충격을 수요/공급 충격의 함수로 나타낸다.

$$ \begin{array}{l}u_{t}^{\pi}=-\sigma_{\pi s} u_{t}^{s}+\sigma_{\pi d} u_{t}^{d}, \\u_{t}^{g}=\sigma_{g s} u_{t}^{s}+\sigma_{g d} u_{t}^{d} \end{array} $$

$$ \Rightarrow \operatorname{Cov}\left(u_{t}^{d}, u_{t}^{s}\right)=0, \operatorname{Var}\left(u_{t}^{d}\right)=\operatorname{Var}\left(u_{t}^{s}\right)=1 $$

 

만약 수요/공급 충격이 heteroskedastic 하다면,

$$ \operatorname{Cov}{t-1}\left[u{t}^{g}, u_{t}^{\pi}\right]=-\sigma_{\pi s} \sigma_{g s} \operatorname{Var}{t-1} u{t}^{s}+\sigma_{\pi d} \sigma_{g d} \operatorname{Var}{t-1} u{t}^{d} $$

 

• 수요 충격 환경이란 $\underbrace{\operatorname{Cov}{t-1}\left[u{t}^{g}, u_{t}^{\pi}\right]>0}_{norminal \ bonds \ hedge \ real \ risk}$이고, 공급 충격 환경이란 $\underbrace{\operatorname{Cov}_{t-1}\left[u_{t}^{g}, u_{t}^{\pi}\right]<0}_{nominal \ bonds \ exacerbrate \ real \ risk}$라고 볼 수 있다.

 

(Non-Guassian shocks)위의 $u_t^{\pi}$ 와 $u_t^g$ 는 Guassian framework 에서 설명할 수 없고 더 높은 차원의 모멘트 즉, 비선형적인 (non-linear) 설명 체계가 필요하다.

 

이때, $E\left[\left(u_{t}^{s}\right)^{3}\right] \approx 0 ; \quad E\left[\left(u_{t}^{d}\right)^{3}\right]<0$ 이라면, Co-skewness 모멘트는 $\sigma_{\pi d}, \sigma_{g d}$ 을 식별할 수 있다.

$$ E\left[u_{t}^{g}\left(u_{t}^{\pi}\right)^{2}\right]<E\left[\left(u_{t}^{g}\right)^{2} u_{t}^{\pi}\right] \Rightarrow \sigma_{\pi d}>\sigma_{g d} $$$$ u_{t}^{d}=\sigma_{p}^{d} \omega_{p, t}^{d}-\sigma_{n}^{d} \omega_{n, t}^{d} $$

 

이때, $\sigma_{p}^{d}$ 는 긍정적인 수요 충격의 크기를, $\sigma_{n}^{d}$는 부정적인 수요 충격의 크기를 나타내며, $\omega_{p, t}^{d}$와 $\omega_{n, t}^{d}$는 de-meaned 감마 분포 de-meaned 감마 분포를 따른다.

 

 

수요 (및 공급) 충격은 “BEGE (Bad Environment– Good Environment)” 로 설명할 수 있다. 우선 수요 충격을 먼저 살펴보면 다음과 같다.

$$ u_{t}^{d}=\sigma_{p}^{d} \omega_{p, t}^{d}-\sigma_{n}^{d} \omega_{n, t}^{d} $$

 

이때, $\sigma_{p}^{d}$ 는 긍정적인 수요 충격의 크기를, $\sigma_{n}^{d}$는 부정적인 수요 충격의 크기를 나타내며, $\omega_{p, t}^{d}$와 $\omega_{n, t}^{d}$는 de-meaned 감마 분포 de-meaned 감마 분포를 따른다.

$$ \begin{array}{l}\omega_{p, t}^{d} \sim \Gamma\left(p_{t-1}^{d}, 1\right) \\\omega_{n, t}^{d} \sim \Gamma\left(n_{t-1}^{d}, 1\right)\end{array} $$

 

이때, n_{t-1}^{d}, n_{t-1}^{d} 는 시간에 따라 변화 (time-varying)하는 파라미터 (parameter)로, 파리미터의 변화로 인해 감마 분포의 형태가 바뀌게 된다.

\begin{array}{|c|c|c|}\hline-\omega_{\mathrm{n}, \mathrm{t}} & & \omega_{\mathrm{p}, \mathrm{t}} \\\hline \mathrm{n}_{\mathrm{t}} & \text { Variance }_{\mathrm{t}} & \mathrm{p}_{\mathrm{t}} \\\hline-2 / \sqrt{\mathrm{n}_{\mathrm{t}}} & \text { Skewness }_{\mathrm{t}} & 2 / \sqrt{\mathrm{p}_{\mathrm{t}}} \\\hline 6 / \mathrm{n}_{\mathrm{t}} & \text { Excess Kurtosis }_{\mathrm{t}} & 6 / \mathrm{p}_{\mathrm{t}} \\\hline\end{array}

 

표에서 알 수 있듯이, 파라미터 값에 따라 충격의 분포 형태, 분산, 비대칭도(skewness), 과잉첨도(excess kurtosis) 등이 변화

 

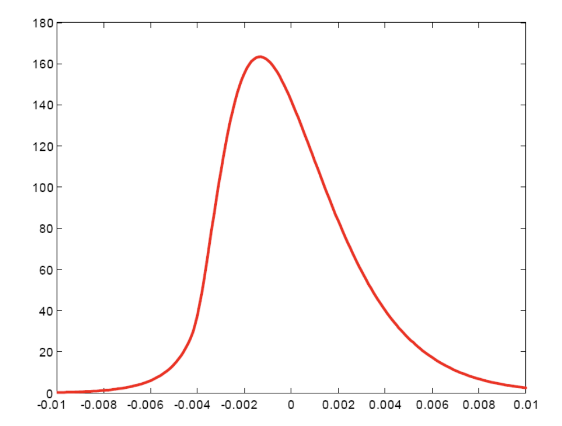
[좌측] Negative skewness: “Bad Environment” (상대적으로 큰 n을 가지는 경우) [우측] Positive skewness: “Good Environment” (상대적으로 큰 p를 가지는 경우)

공급 충격의 조건부 분포는 다음을 통해 설명할 수 있다.

$$ \begin{array}{l}E_{t-1}\left[u_{t}^{S}\right]=0 \\E_{t-1}\left[\left(u_{t}^{S}\right)^{2}\right]=\left(\sigma_{p}^{S}\right)^{2} p_{t}^{S}+\left(\sigma_{n}^{S}\right)^{2} n_{t}^{S} \\E_{t-1}\left[\left(u_{t}^{S}\right)^{3}\right]=2\left(\sigma_{p}^{S}\right)^{3} p_{t}^{S}-2\left(\sigma_{n}^{S}\right)^{3} n_{t}^{S} \\E_{t-1}\left[\left(u_{t}^{S}\right)^{4}\right]-3\left(E_{t-1}\left[\left(u_{t}^{S}\right)^{2}\right]\right)^{2}=6\left(\sigma_{p}^{S}\right)^{4} p_{t}^{S}+6\left(\sigma_{n}^{S}\right)^{4} n_{t}^{S}\end{array} $$

 

[추정 방법론]

데이터는 1962Q2-2016Q4 기간의 분기 데이터를 사용하며, 3가지 step 으로 추정을 한다.

• step1. 실질 경제 활동(unemployment gap 포함)과 물가 (core inflation) 데이터에서 **조건부 평균 (conditional menas)**과 **충격 (Shocks)**을 식별한다. (즉, 데이터로 추정할 수 없는 것과 추정할 수 있는 것들을 골라내는 작업)
• step2. GMM (unconditional) 방법을 활용해서 $u_t^d$ (수요 충격) 및 $u_t^s$ (공급 충격)을 복원시킨다.
  • $\operatorname{Cov}\left(u_{t}^{d}, u_{t}^{s}\right)=0, \operatorname{Var}\left(u_{t}^{d}\right)=\operatorname{Var}\left(u_{t}^{s}\right)=1$ 을 가정하고, $u_{t}^{d}, u_{t}^{s}$ 는 왜도와 첨도를 가지는 데이터이며, $\Sigma(8) ; \Omega(4)$는 파라미터 행렬을 나타낸다.

$$ \left[\begin{array}{l}u_{t}^{s} \\u_{t}^{d}\end{array}\right]=\Sigma^{\prime}\left(\Sigma \Sigma^{\prime}+\Omega \Omega^{\prime}\right)^{-1} u_{t}^{x} $$

• • $u_{t}^{\pi}$: 인플레이션, $u_{t}^{g}$: 경제 성장, $u_{t}^{\pi^{\text{core}}}$: 핵심 인플레이션 , $u_{t}^{u}$: 실업을 의미하고, 결과는 다음과 같다.

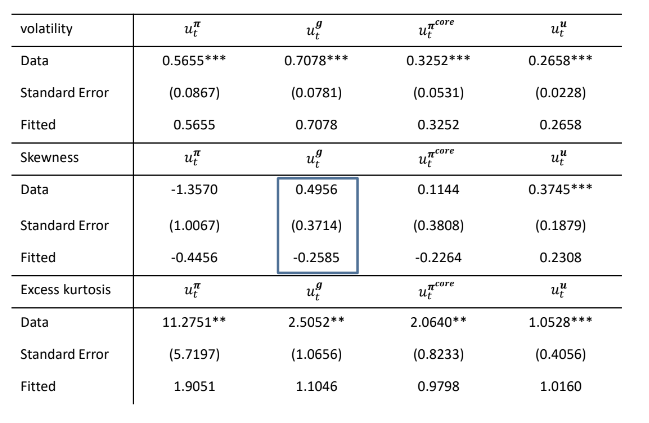
다음으로는 도출된 값을 기반으로 covariance matrix(10), (co)skewness (16), (co)kurtosis (22) 를 추정하고, 결과는 다음과 같다.

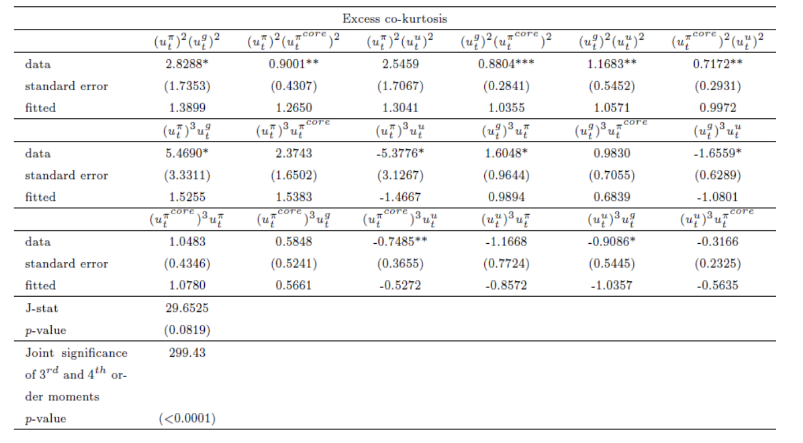
• step3. BEGE 과정을 추정하고 $\left[p_{t}^{d}, n_{t}^{d}, p_{t}^{S}, n_{t}^{s}\right]$ 를 도출한다. (Bates, 2006)
  • 이때, Approximate MLE를 사용해서 거시 변수 요인의 동학을 파악할 수 있다.

 

 

[주요 결과]

(Unconditional) 수요와 공급 충격(표 해석) (Aggregate) 공급 충격의 경우, Skewness 값은 0.0289이다. 이는 약한 양의 비대칭성을 나타내고, Excess Kurtosis 값은 3.3186이며, 이는 과잉첨도를 나타낸다. 과잉첨도가 3보다 크면 뾰족한 꼬리를 가지는 분포를 나타낸다. 수요 충격의 경우, Skewness 값은 -1.4030이며, 이는 강한 음의 비대칭성을 나타낸다. 즉 분포의 꼬리가 좌측에 더 두꺼운 형태를 보인다.

 

$$ \begin{array}{lcc}\hline \text { Shock } & \text { Skewness } & \text { Excess Kurtosis } \\\hline \text { Supply } & 0.0289 & 3.3186 \\& (0.8770) & (1.7417) \\\text { Demand } & -1.4030 & 8.6770 \\& (0.9987) & (4.8979) \\\hline\end{array} $$

 

(표 해석) (Aggregate) 공급 충격의 경우, Skewness 값은 0.0289이다. 이는 약한 양의 비대칭성을 나타내고, Excess Kurtosis 값은 3.3186이며, 이는 과잉첨도를 나타낸다. 과잉첨도가 3보다 크면 뾰족한 꼬리를 가지는 분포를 나타낸다. 수요 충격의 경우, Skewness 값은 -1.4030이며, 이는 강한 음의 비대칭성을 나타낸다. 즉 분포의 꼬리가 좌측에 더 두꺼운 형태를 보인다.

 

(그림 해석) 여기서 70년대의 경기 침체는 음의 공급 충격으로부터 비롯되었다는 점을 파악할 수 있다. 즉, 생산성의 감소나 자원 부족 등의 문제로 경기 침체가 일어났었음을 예측해볼 수 있다. 대공황 (Great Recession)은 대부분 수요 충격이 원인이었지만 공급의 충격 (4번째 그림의 2007-2010 부분) 도 어느 정도 있었음을 확인할 수 있다.

 

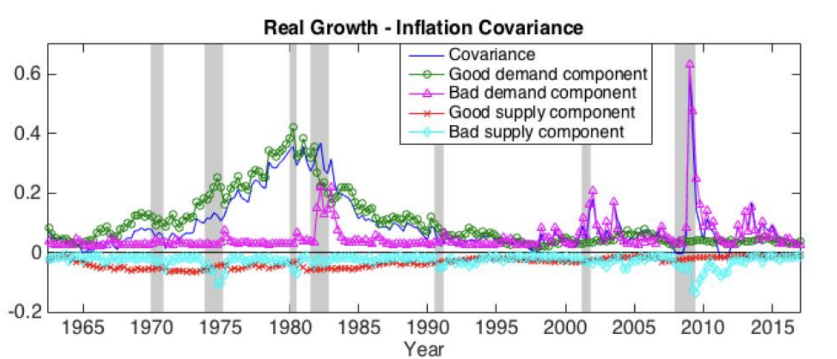
위에서 p_{t}^{d}, n_{t}^{d}, p_{t}^{S}, n_{t}^{s} 를 도출했고 u_t^s, u_t^d 도 도출해 냈다. 이제는 두번째로, 매크로 위험과 기간 구조를 연결시키는 것이다.

 

 

[Macro risk 와 Term Structure]

매크로의 요인들의 채권 수익률 설명력을 다음과 같이 Adjusted $R^2$ 값을 통해 나타내 보았다.

 

$$ \begin{array}{lccc} & \frac{1 \text { year bond }}{} & & \frac{5 \text { year bond }}{} \\\text { 3 financial factors } & 6.66 \% & 7.08 \% \\\text { 3 financial factors + macro level factors } & 9.62 \% * & 7.74 \% \\\text { 3 financial factors + macro risks } & \mathbf{1 3 . 3 8 \% * * *} & \mathbf{1 1 . 0 1 \% * *} \\\begin{array}{l}\text { 3 financial factors + macro level factors + } \text { macro risks }\end{array} & \mathbf{1 4 . 2 9 \% * *} & \mathbf{1 0 . 6 5 \% *}\end{array} $$

 

(표 해석) 매크로 (수준) 요인들이 금융 요인보다 초과 채권 수익률 (Excess Bond Return)의 추가적인 설명력 (Explanatory power)을 더 가지고 있음을 확인할 수 있다. 또한 3가지 금융 요인에 매크로 수준 요인과 매크로 리스크 요인을 모두 추가한 경우의 1년 만기 채권의 수익률이 설명력이 가장 높았다는 점을 알 수 있다.

 

다음으로 채권의 수익률 (리스크 프리미엄)에 대해 매크로의 요인들을 회귀분석 (regression) 했을 때 다음과 같은 결과값을 도출할 수 있다.

	1 year bond	5 year bond
$p_t^d$	0.87***	3.15***
$n_{t}^{s}$	0.23***	1.66***
$p_{t}^{s}, n_{t}^{s}$	positive, mostly insignificant coefficients	positive, mostly insignificant coefficients

이때, 더미에 속해 있는 내재된 리스크 프리미엄은 demand-supply variance ratio 이다.