Credit, capital and crises: a GDP-at-Risk approach

 

 

 

Quantile 회귀분석을 사용하여 중장기적으로 성장에 대한 하향 리스크, GDP-at-Risk,가 거시적 안정성에 어떻게 영향을 받는지 하나하나 뜯어나간다.

 

제목 : Credit, capital and crises: a GDP-at-Risk approach (2019)
저자 : David Aikman, Jonathan Bridges, Sinem Hacioglu Hoke, Cian O’Neill and Akash Raja
저널 : Bank of England

 

 

우선, 여러 가지 취약성 지표가 GDP 분포에 미치는 영향을 살펴보고, 2) 초점은 GDP 분포의 꼬리인 GDP-at-risk와 그 중기적인 (3-5년 전망) 결정 요인을 살펴보고, 3) 금융 시스템의 탄력성 부족이 경제 성장의 하락 위험과 연결될 수 있음을 보여준다. 나아가 4) 은행 자본의 증가가 중기적으로 GDP-at-risk을 개선할 수 있음을 보여주기도 한다.

 

 

데이터는 16개 선진국을 대상으로 한 패널 데이터를 활용하고,

• credit booms, property price booms 및 광범위한 통화 수지 적자 (current account deficits)가 3-5년 간격(horizon)으로 성장에 상당한 하향 리스크를 초래한다는 것을 발견
  • 특히, 최악의 GDP 재앙이라고 볼 수 있는 신용 붐은 이 재앙 전 75%에 선행해서 나타나는데, 중기적으로 GDP-at-risk를 매우 증가시킨다.

 

• 은행 시스템(banking system)의 자본화(capitalisation)를 늘리면 이러한 하향 리스크를 일부 완화할 수 있다는 것을 발견
  • 은행 자본을 늘리는 것이 3년 동안의 GDP 성장 분포의 5th 백분위수로 정의된 GDP-at-Risk에 대한 평균적인 약화를 4.5 백분율 정도 완화할 것으로 추정
  • countercyclical capital buffer rate이 2.5%(5%)와 동등하게 하는 은행 자본 증가는, 중장기적인 거시경제적 꼬리 리스크 증가의 약 20%(40%)까지 완화(mitigate)하는 데 충분하다는 것을 qunatitive하게 보여줌

 

 

 

[데이터]

(1) 다섯 가지 취약성 지표에 대한 시계열

• 다양한 유형의 신용 (부문별, 대출 유형별), 부채상환 능력 (debt serviceability)및 특정 수준의 부채의 분포
  • (1) 민간 비은행 금융부문 credit-to-GDP 의 3년 동안 비율 변화(percentage point change) (3yr change)
  • (2) 3년 동안의 실질 주택 가격 (real house price) 상승률 (3yr growth)
  • (3) GDP 대비 통화 수지 적자 (current account deficit) 비율(% of GDP)
  • (4) 1분기 동안의 주가 변동성
  • (5) 금융 시스템의 회복 탄력성 (resilience) - banking system tangible common equity (TCE) to total asset ratios
    • Firm-level 에서의 TCE (자본 - 우선주 및 무형자산)
    • 총 유형 자산(tangible assets)에 대한 개별 은행의 재무상태 데이터

(2) 은행 자본 (Bank Capital)

• TCE 비율을 구하기 위해서, 각 국가의 (1) 기업 수준의 TCE (자본에서 우선주 및 무형자산을 뺀 것)와 (2) 총 유형자산에 대한 개별 은행의 재무제표 데이터 활용
  • number of banks per year
  • Market capitalisation ($m)
  • Tangible assets (billions NOK) ⇒ total tangible assets at the bank level 총 자산 - 무형자산
  • Aggregate total assets (billions NOK)
• TCE ratio = 유형 자본 / 유형 자산
• 국가별 TCE ratio로 데이터를 집계하기 위해 chain-weighted 방법을 사용하며, 각 기간의 은행의 참여와 이탈을 고려
• 선형 보간을 사용하여 분기별 시계열을 만듦

 

(3) Financial Condition

• 금융 시장의 volatility 를 proxy 변수로 사용

---

 

[기본적인 현상 및 데이터]

(GDP catastrophes)

 

 

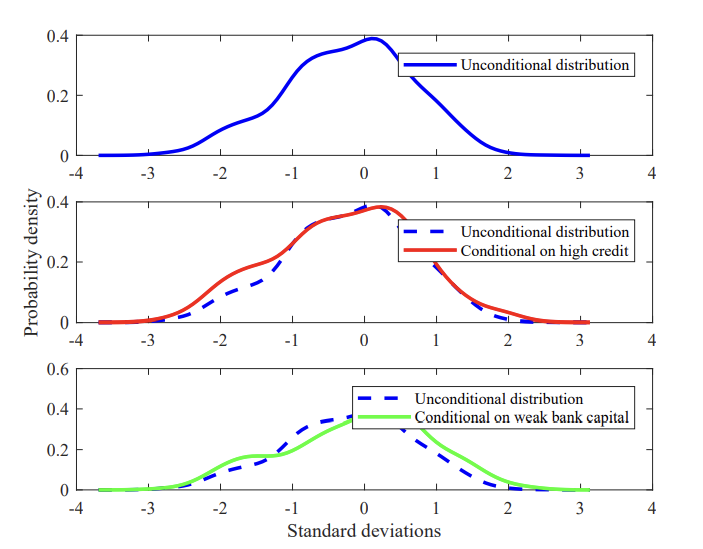
패널은 데이터셋 내 모든 16개 국가에 대해 통합된 3년간 실제 GDP 성장률 (1) 무조건적 분포 (2) 3년간의 credit-to-GDP 성장이 12분기 전에 국가별 평균을 초과한다는 조건 (3) TCE 비율이 12분기 전에 국가별 평균 미만인 조건 하

커널 밀도 추정기를 사용하여 추정했고, 3년 성장률을 중점적으로 다루어 분기 또는 연간 주기의 노이즈 있는 관측을 걸러내고 오히려 지속적인 감소에 중점을 둔다.

• 이때, gdp 성장률은 보통 왼쪽으로 치우친 형태를 띄고 있으며, 정규 분포에서 예상되는 것보다 왼쪽 꼬리가 더 긴 특징
• credit-to GDP 성장이 12분기 전에 국가별 평균을 초과한다는 조건 하에 실제 GDP 성장의 분포의 확률 질량이 더 왼쪽 꼬리로 이동

 

 

(국가 패널 데이터) 극단적인 상황에서의 취약성과 성장 간의 관계에 중점을 두기 위해, 데이터 셋을 정렬하고 3년 동안 실제 GDP의 가장 큰 감소가 언제 일어났는지를 찾는다.

 

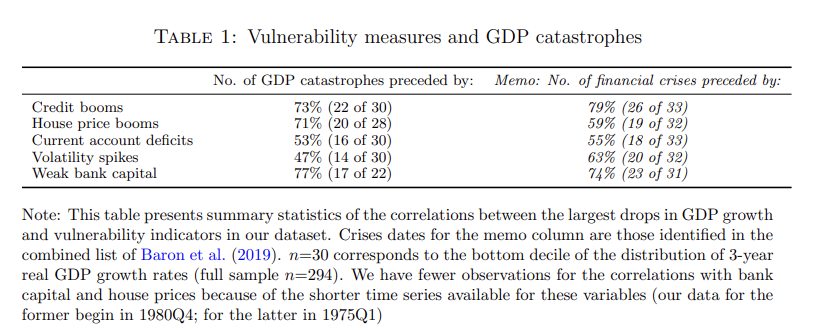
GDP 재앙 전 취약성 (지표로 측정한)이 선행한 경우의 비율

실제 GDP의 가장 심각한 감소 중 30개 중 22개 (73%)는 GDP 감소의 시작 시점으로부터 신용 붐에 의해 먼저 선행이 됨

• 신용 붐 정의는 credit-to-GDP의 3년 성장률이 해당 국가의 평균을 초과할 때
• 즉, 세 번 중 두 번의 credit boom은 은행 위기 또는 장기간의 부적합한 성장으로 이어질 수 있다.

 

빨간색 점은 샘플에서, GDP 감소가 가장 크게 일어난 30가지 경우를 나타냄

신용 붐의 경우, 빨간색으로 표시된 대부분의 점이 실제로 남동쪽 (신용 성장)과 남서쪽 (은행 자본) 사분면에 위치하는 것은 Table 1과 일치한다고 볼 수 있다.

• 분명히 GDP 재앙은, ‘미미한 것으로 보이는’ 취약성 증가와 연결이 되어 있음
• 신용 붐이나 자본이 약화된 은행 시스템에 선행되지 않은 GDP 붕괴 (타입 1 오류)를 살펴보면, 이러한 경우 중 많은 부분이 금융 불안과 관련이 없는 요소로 인한 경제 침체라는 것도 확인이 가능하다.

 

 

[방법론]

선진국들의 패널에 대해 quantile-regression분석을 추정하며, 추정 편향(estimation bias)을 피하기 위해 국가별 고정 효과(country-specific fixed effects)를 처리(treatment) 해주어야 한다.

 

 

 

고정 효과를 없애는 두 가지 방법

 

(1) 표준 within estimator를 사용하여 고정 효과를 추정

 

우선, pooled panel model by OLS는 다음과 같다.

• 실제 GDP 연평균 성장률 $y_{i, t+h}=\frac{\left(Y_{i, t+h}-Y_{i, t}\right)}{h / 4}$ 는 log level of real GDP (h=1,…,20Q)
• $\alpha_{i}^{h}$ 는 고정 효과를 보여주며, $X_{i t}$ 는 취약성 지표 및 국가 i 의 시간 t 에서 측정된 Control 변수가 포함
  • 취약성 지표에는 credit-to-GDP 등 포함
  • control 변수로는 인플레이션률, 중앙 은행의 연간 금리 변동률 및 이전 시점의 GDP 성장률을 포함

$$ y_{i, t+h}=\alpha_{i}^{h}+\gamma^{h} X_{i, t}+\epsilon_{i, t} $$

 

 

(2) 두 번째 단계에서 우리는 종속 변수를 $y_{i, t+h}^{*}=y_{i, t+h}-\hat{\alpha}_{i}^{h}$ 로 정의하고, 첫 번째 단계 종속 변수에서 추정된 국가 고정 효과를 빼게 된다.

• 이제 분위 회귀를 이용해서 $\beta_{\tau}^{h}$ 를 추정
  • $\rho_{\tau}$ 표준 비대칭 절대 손실 함수 (standard asymmetric absolute loss function)

$$ \hat{\beta}{\tau}^{h}=\operatorname{argmin}{\beta^{h}} \sum_{i, t} \rho_{\tau}\left(y_{i, t+h}^{*}-X_{i, t} \beta_{\tau}^{h}\right) $$